Test de la dérivée première - Définition
Le test de la dérivée première consiste à calculer la dérivée d'une fonction pour la tester ensuite.
En trouvant les points où la dérivée est nulle, il est possible de déterminer les extrema et les points d'inflexion horizontaux de la première fonction. Dans un graphique, les points où la dérivée est nulle se trouvent soit sur un plateau, soit sur un minimum/maximum local, soit sur un point d'inflexion horizontal. Celui-ci peut être global.
Il y a trois endroits où une fonction peut avoir un maximum ou un minimum, absolu ou relatif.
- Aux bornes du domaine de la fonction
- Aux points où la tangente est horizontale ( f'(x) = 0 )
- Aux points où la tangente est verticale ( f'(x) n'existe pas )
Exemple
Soit la fonction f(x) = 2x3 − 3x2 − 12x + 10. Utilisons le test de la dérivée première pour obtenir les extremums, pour éventuellement tracer le graphe de f(x).
Identifions les valeurs critiques
Posons f'(x)
Posons f'(x) = 0 pour identifier quand la tangente est horizontale.
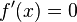
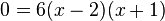
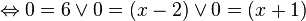
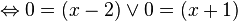
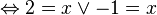
Donc, la tangente est horizontale en x=2 et x=-1
Vérifions quand f'(x) n'existe pas
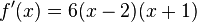
On en déduit qu'une dérivée existe pour toute valeur de x.
Tableau de valeurs
| x |
|
-1 | ... | 2 |
|
| f'(x) | + | 0 | - | 0 | + |
| f(x) |
|
17 |
|
-10 |
|
Donc, comme 17 se trouve dans un " pic " de la fonction, c'est un maximum relatif. Et comme -10 se trouve dans un " creux " de la fonction, c'est un minimum relatif.
En conclusion
Le test de la dérivée première est utile pour trouver les extremums et les points d'inflexion horizontaux d'une fonction.