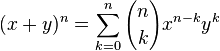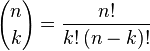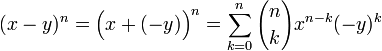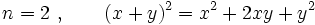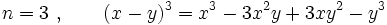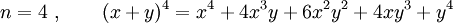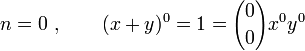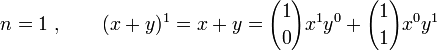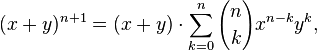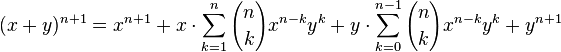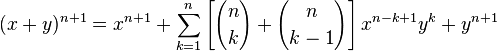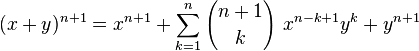Formule du binôme de Newton - Définition

Le binôme de Newton est une formule de mathématiques donnée par Isaac Newton pour trouver le développement d'une puissance entière quelconque d'un binôme. Il est aussi appelé formule du binôme de Newton, ou plus simplement formule du binôme.

Énoncé

Soit un binôme composé des termes x et y défini sur un anneau (tels que xy=yx), et un entier naturel n,

où les nombres

(parfois aussi notés ) sont les coefficients binomiaux.

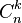
Remplacer dans la formule y par -y revient à prendre le second terme comme négatif :

Exemple :

Démonstration

Soient x, y des éléments d'un anneau tels que xy=yx et n un entier naturel.

Démontrons cette formule par récurrence.

Initialisation

Hérédité

Soit n un entier supérieur ou égal à 1, montrons que si la relation est vraie pour n, elle l'est aussi pour n+1 :

Par hypothèse de récurrence :

Par distributivité de sur +  :

Par factorisation :

En utilisant la formule du triangle de Pascal :

Ce qui termine la démonstration.