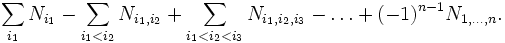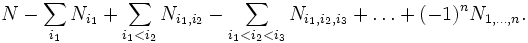Principe d'inclusion-exclusion de Moivre - Définition

Exemple d'inclusion-exclusion à partir de trois ensembles

En combinatoire, le principe d’inclusion-exclusion de Moivre permet d’exprimer le nombre d’éléments qui satisfait l’une ou l’autre propriétés données, en fonction du nombre de ses éléments qui satisfont à la fois certaines de ses propriétés.

Il doit son nom au mathématicien Abraham de Moivre.

Théorème

Soit E un ensemble fini, dont chaque élément peut ou non satisfaire certaines de n propriétés . Notons le nombre d’éléments de E qui vérifient les propriétés (et éventuellement d’autres propriétés). Alors le nombre N d’éléments (distincts) de E qui satisfont à l’une ou l’autre de ces propriétés est donné par

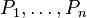
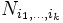
De façon équivalente, le nombre d’éléments de E qui ne vérifient aucune propriété est égal à

Cas particulier

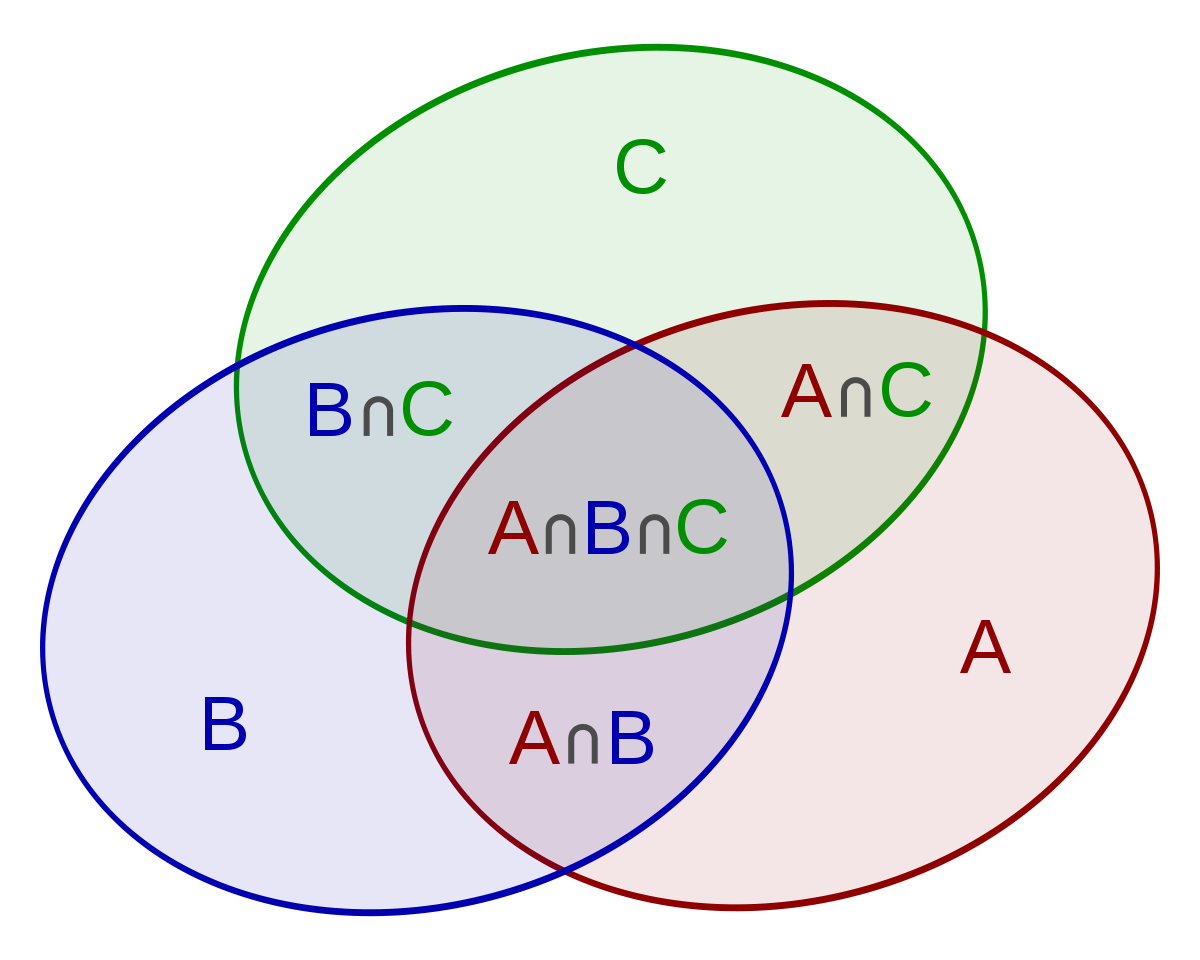
Considérons le cas particulier où n=2. Soit E un ensemble fini, dont chaque élément peut ou non satisfaire l’une ou l’autre des deux propriétés P₁ et P₂. Notons

• N₁ le nombre d’éléments de E qui vérifient P₁,
• N₂ le nombre d’éléments de E qui vérifient P₂,
• N_1,2 le nombre d’éléments de E qui vérifient à la fois P₁ et P₂.

Alors le nombre N d’éléments de E qui satisfont à l’une ou l’autre de ces propriétés est égal à

N = N₁ + N₂ − N_1,2.

Autrement dit, le nombre d’objets vérifiant l’une ou l’autre de ces deux propriétés est égal à la somme des nombres d’objets vérifiant chaque propriété diminuée du nombre d’objets possédant à la fois les deux propriétés.

Exemple

Parmi 20 étudiants, 10 étudient les mathématiques, 11 étudient la physique, et 4 étudient les deux. Combien y a-t-il d’étudiants qui n’étudient ni les mathématiques ni la physique ?

Pour visualiser nous pouvons construire un diagramme de Venn.

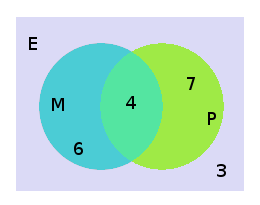
Nous entourons les éléments qui vérifient la même propriété. E représente le groupe entier d’étudiants, M représente ceux qui ont la propriété d'" étudier les mathématiques ", P représente ceux qui possède la propriété : d'" étudier la physique ".

Nous plaçons dans chaque partie le nombre d’étudiants. Étant donné que quatre personnes étudient à la fois les mathématiques et la physique, nous reportons un 4 dans l’intersection des deux cercles. Nous devons donc avoir 10-4=6 personnes qui étudient les mathématiques mais pas la physique et 11-4=7 personnes qui étudient la physique mais pas les mathématiques. Il reste donc 20-(6+4+7)=3 personnes qui n’étudient ni les mathématiques ni la physique.

Ce résultat se retrouve facilement en utilisant le principe d’inclusion-exclusion qui donne le nombre d’étudiants ne possédant pas ces deux propriétés 20-10-11+4=3.

Applications

Le principe inclut aussi des inégalités, montrant que la somme des premiers termes de la formule est alternativement un majorant et un minorant du premier membre. Ces inégalités peuvent être utilisées dans les cas où la formule complète est trop encombrante.

Le principe d’inclusion-exclusion se retrouve dans la formule du crible de Poincaré et la formule du crible de Poincaré en probabilité ou dans la formule d'inversion de Möbius.