Diagramme de Venn - Définition

Les diagrammes de Venn et les diagrammes d'Euler sont des représentations schématiques d'ensembles, de relations logiques ou mathématiques.

Diagrammes de Venn, Euler et Johnston

Considérons C={C₁, …, C_n}, un ensemble de courbes fermées simples du plan. C est un diagramme de Venn, ou un n-diagramme de Venn, si toutes les intersections d'une région intérieure (ou extérieure) délimitée par une courbe, avec une région intérieure (ou extérieure) délimitée par une autre courbe sont non vides et connexes, et si de plus il n'y a qu'un nombre fini de telles intersections.

Soit C={C₁, …, C_n}, un ensemble de courbes fermées simples du plan. C est un diagramme d'Euler, si toutes les intersections d'une région intérieure (ou extérieure) délimitée par une courbe, avec une région intérieure (ou extérieure) délimitée par une autre courbe sont connexes, et si de plus il n'y a qu'un nombre fini de telles intersections.

La différence entre un diagramme d'Euler et un diagramme de Venn réside uniquement dans la possibilité, pour des intersections de régions délimitées par les courbes, d'être vides. Un diagramme de Venn est donc un cas particulier de diagramme d'Euler.

Les diagrammes de Venn, de Johnston, et d'Euler peuvent sembler identiques en apparence. Leurs différences apparaissent dans leurs domaines d'application suivant le type d'ensemble qui doit être partitionné.

Les diagrammes de Johnston sont adaptés à la représentation des valeurs de vérité des propositions logiques, tandis que les diagrammes d'Euler servent à illustrer des ensembles spécifiques d'objets et les diagrammes de Venn sont généralement utilisés pour mettre en évidence de possibles relations.

En analyse des syllogismes, les régions des diagrammes de Venn sont coloriées lorsqu'elles ne contiennent pas d'élément et de cette façon ils permettent de représenter tous les systèmes d'ensembles, ce qui est plus difficile avec des diagrammes d'Euler compte tenu du fait que les régions ne contenant pas d'élément ne sont pas représentées.

En fait, Euler a essayé de montrer les rapports entre des ensembles spécifiques, tandis que Venn a voulu représenter tous les partitionnements possibles des ensembles.

Ces concepts de diagramme d'Euler et de Venn, n'ont pas été " unifiés " et attribués à Euler, probablement parce qu'Euler a introduit ses diagrammes 100 années plus tôt, et était déjà l'auteur de beaucoup de travaux.

Représentations graphiques de diagrammes de Venn

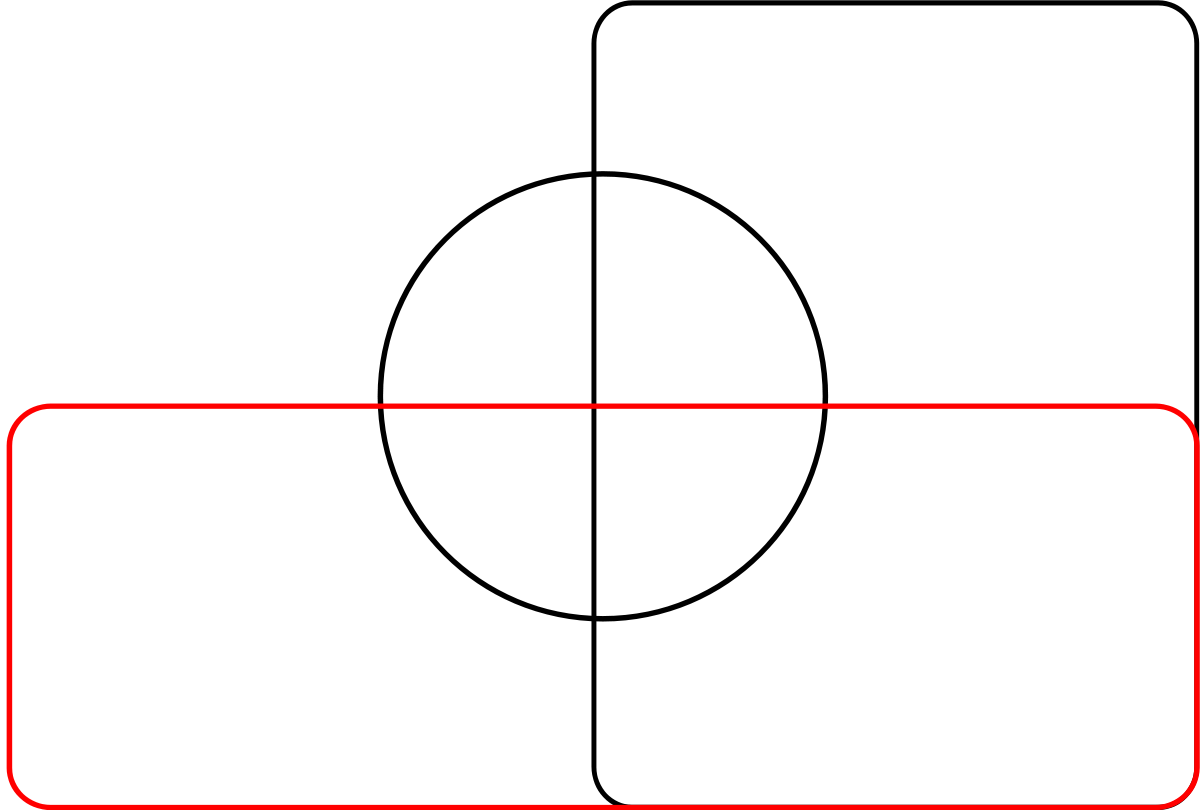
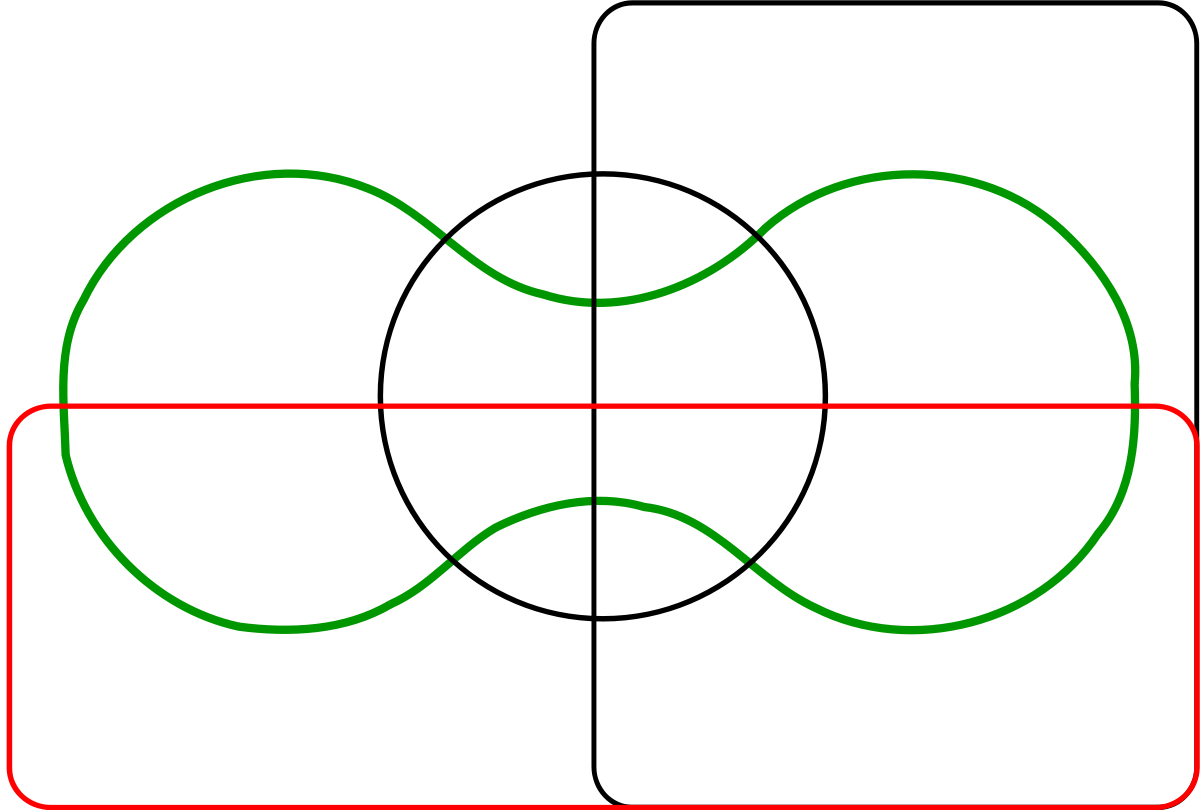
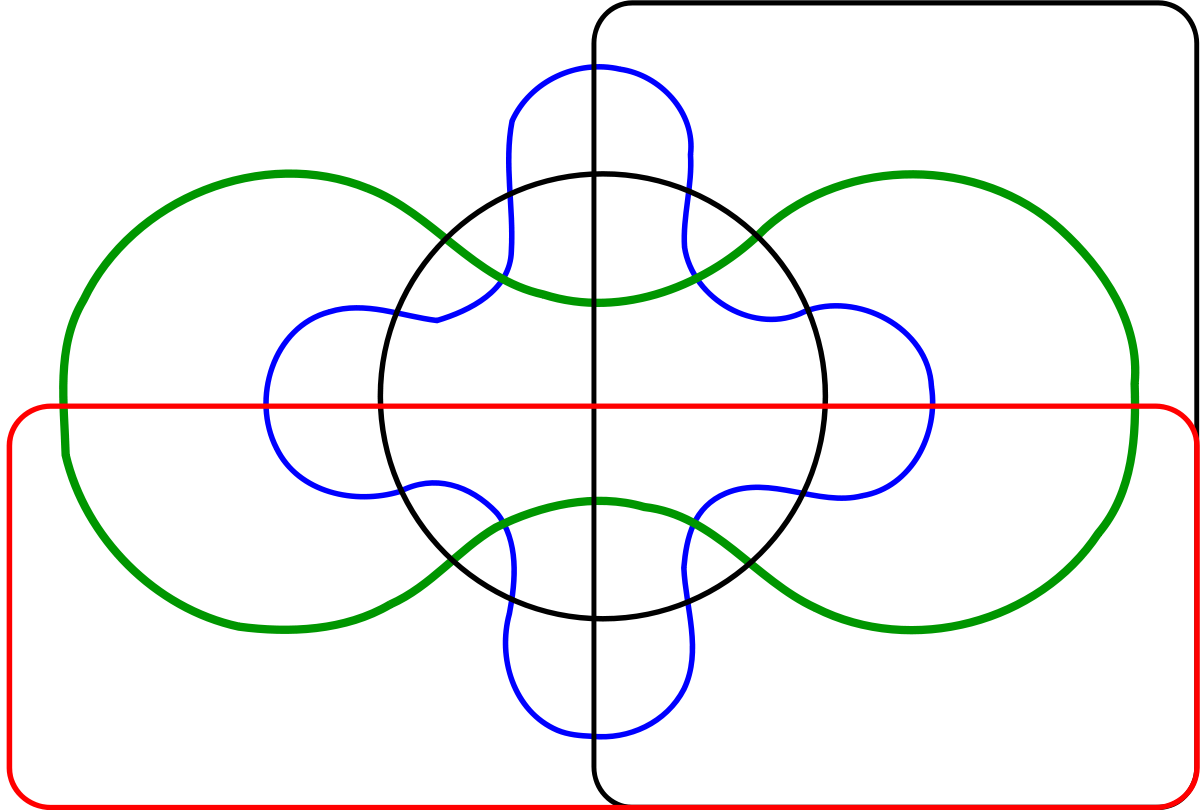
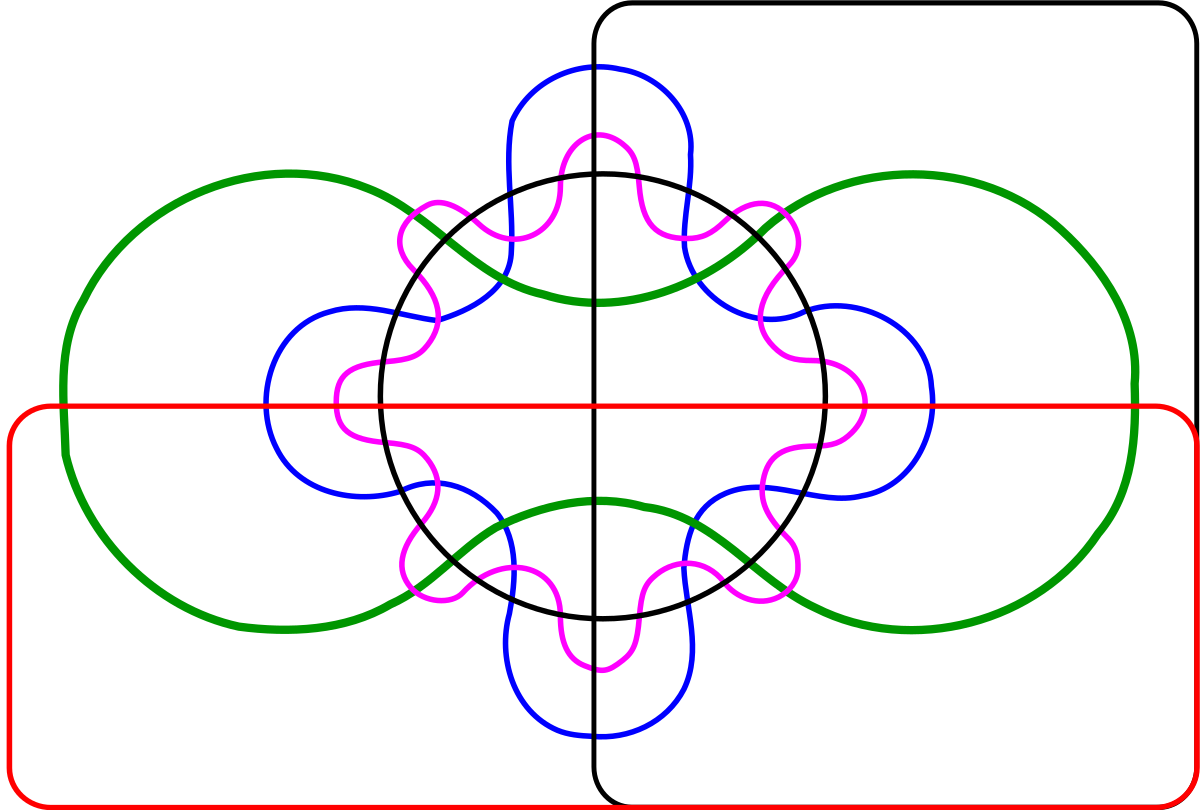
La difficulté consiste souvent à trouver une représentation graphique agréable d'un diagramme de Venn. Rappelons qu'un diagramme de Venn à n ensembles doit partager le plan en 2ⁿ zones, c'est-à-dire 4 zones pour 2 ensembles, 8 pour trois ensembles, 16 pour quatre...

Autant il est simple de représenter un diagramme de Venn à deux ensembles (deux courbes fermées) ou même à trois (trois cercles de rayon R dont les centres forment un triangle équilatéral de côté R), autant la situation se complique pour la représentation d'un diagramme de Venn à quatre ensemble, voire 5. Venn lui même n'a jamais été satisfait de sa représentation de 5 ensembles. Il faut attendre près d'un siècle avant que le généticien et statisticien A.W.F. Edwards n'en propose une représentation élégante dans son livre Cogwheels of the Mind

Diagramme de Venn à trois ensembles		Diagramme de Venn à quatre ensembles
Diagramme de Venn à cinq ensembles		Diagramme de Venn à six ensembles
Ref: Ian Stewart Another Fine Math You've Got Me Into 1992 ch4