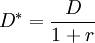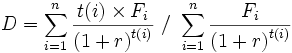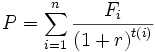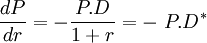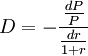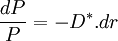Duration - Définition
La duration d'un instrument financier à taux fixe, comme une obligation, est la durée de vie moyenne de ses flux financiers pondérée par leur valeur actualisée. Toutes choses étant égales d'ailleurs, plus la duration est élevée, plus le risque est grand.
Utilisation
Il s'agit d'un outil permettant de comparer schématiquement plusieurs instruments ou obligations à taux fixe entre eux, quelles qu'aient été leurs conditions d'émission. C'est essentiellement une mesure patrimoniale statistique, qui fournit aux gestionnaires de fonds ou aux gestionnaires d'actif/passif une grandeur qu'ils vont comparer à la durée moyenne d'un mandat de gestion, ou à une durée moyenne d'emploi des fonds.
Elle est utilisée avant tout pour immuniser des portefeuilles, comme succédané simple mais efficace :
- soit d'un adossement parfait, flux financier par flux financier, avec des obligations zéro-coupon, souvent difficile à réaliser;
- soit d'une modélisation mathématique fiable de l'évolution sur une longue période de la courbe des taux d'intérêt .
Comme, par définition, la duration est inférieure à la durée de vie moyenne simple (c’est-à-dire pondérée uniquement par les flux de remboursement du capital, non actualisés) de l'obligation, son emploi amène à couvrir systématiquement un passif par une obligation de durée plus longue.
En effet, si la durée du passif est M, une obligation de duration N aura nécessairement une durée de vie moyenne N
La duration est parfois présentée péremptoirement comme "la durée qu'une obligation met à rembourser son prix d'achat". Cela n'est entièrement vrai que dans le cas d'instruments zéro-coupon. Pour toutes les autres obligations, cette définition est à prendre avec une grande pincée de sel, car elle omet qu'il s'agit d'une valeur moyenne...
Confusions à éviter
La duration donne en revanche une mesure plutôt approximative de l'impact instantané d'une variation des taux d'intérêt sur le prix de cette obligation. Certes, plus la duration est grande, plus l'impact sur le titre le sera. Néanmoins, cette mesure est trop imprécise pour être utilisée sur les marchés financiers.
Par ailleurs, elle ne tient pas compte de la forme de la courbe des taux, ni de ses déformations, ni de sa dynamique.
Duration modifiée
Le terme de "modified duration" dans la littérature anglo-saxonne désigne la formule suivante:
La duration modifiée mesure la sensibilité d'un produit aux variations de taux d'intérêts. Tandis que la duration mesure cette sensibilité en absolue, la duration modifiée la mesure en pourcentage.
Formulation mathématique
La duration
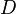
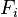
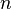
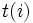
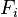
avec

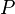
On remarque (cf ci-dessus, Confusions à éviter) que la mesure du risque de taux instantané,
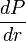
mais en est bien différente.
Autrement dit, la duration est l'élasticité (au signe près) du prix de l'obligation au taux actuariel :