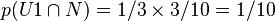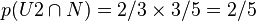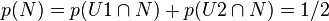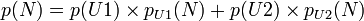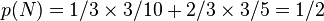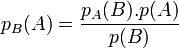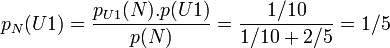Arbre de probabilité - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
En probabilité élémentaire, un arbre de probabilité est un schéma permettant de résumer une expérience aléatoire connaissant des probabilités conditionnelles
Exemple
On cherche à résumer l'expérience aléatoire suivante :
- On lance un dé
- Si le numéro obtenu est un multiple de 3, on extrait au hasard une boule dans l'urne 1 qui contient 3 boules noires, 4 boules blanches et 3 boules rouges
- Si le numéro obtenu n'est pas un multiple de 3, on extrait une boule dans l'urne 2 qui contient 3 boules noires et 2 boules blanches.
La première étape permet de définir un univers Ω = {1 ; 2 ; 3 ; 4 ; 5 ; 6} sur lequel on applique une équiprobabilité (on estime le dé parfaitement équilibré). On considère alors les deux évènements complémentaires
- U1 = " le lancer conduit à tirer dans l'urne 1 "
- U2 = " le lancer conduit à tirer dans l'urne 2 "
On a donc U1 = { 3 ; 6 } et p(U1) = 1/3 puis p(U2) = 2/3.
Pour étudier la seconde étape, il faut étudier ce qui se passe quand on tire dans l'urne 1 ou l'urne 2.
- Le tirage dans l'urne 1 permet de définir un univers Ω1={N ; B ; R} sur lequel on applique la probabilité suivante
- p(N) = 3/10
- p(B) = 4/10
- p(R) = 3/10.
- Il s'agit en réalité du transfert à Ω1 d'une équiprobabilité définie sur Ω1'={N, N, N, B, B, B, B, R, R, R}.
- De même, le tirage dans l'urne 2 permet de définir un univers Ω2={N, B} de probabilités 3/5 et 2/5.
L'expérience se résume alors dans l'arbre suivant:
La lecture des probabilités se fait alors aisément:
- Probabilité de tirer dans l'urne 1 et d'obtenir une noire :
- Probabilité de tirer dans l'urne 2 et d'obtenir une noire :
La probabilité de tirer une boule noire est alors :
Définitions et propriétés
Un arbre de probabilité est un graphe orienté et pondéré obéissant aux règles suivantes
- La somme des pondérations (ou probabilités) des branches issues d'un même sommet donne 1.
- La probabilité d'un chemin est le produit des probabilités des branches qui le composent.
- La pondération de la branche allant du sommet A vers le sommet B est la probabilité conditionnelle de B sachant que A est déjà réalisé pA(B).
On retrouve alors la propriété de la probabilité conditionnelle :
-
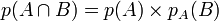
Ainsi que la formule des probabilités totales:
- si Ω1, Ω2, ..., Ωn définit une partition de Ω (ensembles deux à deux disjoints dont l'union donne Ω), si les Ωi sont de probabilité non nul, et si A est un évènement de Ω,
-
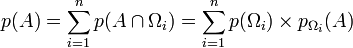
Que l'on a exploitée dans l'exemple pour calculer p(N)
L'arbre de probabilité facilite aussi l'inversion des probabilités conditionnelles ou théorème de Bayes :
Dans l'illustration précédente, cela revient à poser la question : " Sachant que l'on a tiré une noire, quelle est la probabilité que l'on ait tiré dans l'urne 1? "