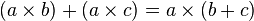Distributivité (mathématiques élémentaires) - Définition

La distributivité est une propriété de la multiplication qui permet d'effectuer de deux manières différentes le produit d'un nombre par une somme :

Ici on a distribué a à chaque terme de la somme

Ici on a distribué c à chaque terme de la somme

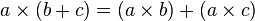
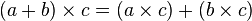
Passer du produit d'un nombre par une somme à une somme de deux produits s'appelle développer l'expression.

En écrivant l'égalité dans l'autre sens, on obtient alors la mise en évidence ou factorisation :

Ici on a mis a en facteur dans l'expression