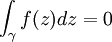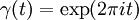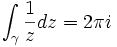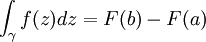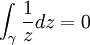Théorème intégral de Cauchy - Définition
En analyse complexe, le théorème intégral de Cauchy est un important résultat concernant les intégrales curvilignes de fonctions holomorphes dans le plan complexe. D'après ce théorème, si deux chemins différents relient les deux mêmes points et si une fonction est holomorphe " entre " les deux chemins, alors les deux intégrales de cette fonction suivant ces chemins sont égales.
Le théorème est habituellement formulé pour les chemins fermés de la manière suivante : soit U un sous-ensemble ouvert de 
qui est simplement connexe, soit 
une fonction holomorphe, et soit γ un chemin rectifiable dans U dont le point de départ est confondu avec le point d'arrivée (c'est-à-dire un lacet), alors :
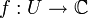
Comme cela a été montré par Goursat, le théorème intégral de Cauchy peut être démontré en supposant seulement que la dérivée complexe de f existe en tout point de U. Ceci est très intéressant, parce que nous pouvons alors démontrer la formule intégrale de Cauchy pour ces fonctions, et de cela nous pouvons déduire que ces fonctions sont en fait indéfiniment continûment dérivables.
La condition que U est simplement connexe signifie que U n'a pas de " trou " ; par exemple, tout disque ouvert 
satisfait à cette condition. La condition est cruciale; par exemple, si γ est le chemin défini par :
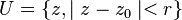
où exp est la fonction exponentielle, qui décrit le cercle unité, alors l'intégrale sur ce chemin
est non nulle ; le théorème intégral de Cauchy ne s'applique pas ici puisque f(z) = 1/z n'est pas défini (et donc f n'est certainement pas holomorphe) en z = 0.
Une conséquence importante du théorème est que l'intégrale curviligne de fonctions holomorphes sur des domaines simplement connexes peut être calculée d'une manière familière à partir du théorème fondamental du calcul différentiel et intégral : soit U un ouvert simplement connexe de , soit une fonction holomorphe, et soit γ un chemin continûment différentiable dans U dont le point de départ est a et le point d'arrivée b. Si F est une primitive complexe de f, alors
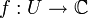
Le théorème intégral de Cauchy est valable sous une forme légèrement plus forte que celle donnée ci-dessus. Supposons que U soit un ouvert simplement connexe de dont la frontière est l'image du chemin rectifiable γ. Si f est une fonction qui est holomorphe sur U et continue sur l'adhérence de U, alors
Le théorème intégral de Cauchy est considérablement généralisé par le théorème des résidus.
Surfaces de Riemann
Le théorème intégral de Cauchy se généralise dans le cadre de la géométrie des surfaces de Riemann.