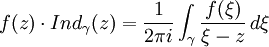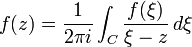Formule intégrale de Cauchy - Définition
La formule intégrale de Cauchy est un point essentiel de l'analyse complexe. Elle exprime le fait que la valeur en un point d'une fonction holomorphe est complètement déterminée par les valeurs qu'elle prend sur un chemin fermé contenant ce point. Elle peut aussi être utilisée pour exprimer sous forme d'intégrales toutes les dérivées d'une fonction holomorphe.
Expression
Supposons que U soit un ouvert connexe du plan complexe
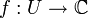
Cette formule est particulièrement utile dans le cas où γ est un cercle C orienté positivement, contenant z et inclus dans U: on peut alors écrire:
Principale conséquence
Montrons que ceci implique que f est développable en série entière sur U : soit
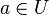
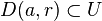
Soit
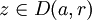
![\theta\in[0,2\pi]](https://static.techno-science.net/illustration/Definitions/autres/b/b1194bd0172849450c424366d14501a0_2aa31e38b4269ff4d39f584e1a69e668.png)
On a pour tout
![\theta\in[0,2\pi]](https://static.techno-science.net/illustration/Definitions/autres/b/b1194bd0172849450c424366d14501a0_2aa31e38b4269ff4d39f584e1a69e668.png)
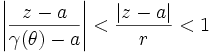
ce qui prouve la convergence uniforme sur [0,2π] de la série de terme général
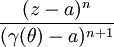
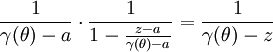
et comme
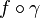
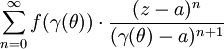
ce qui permet d'effectuer une inversion des signes sommes: on a ainsi pour tout z dans D(a,r):
-
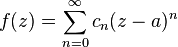
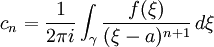
et donc f est analytique sur U. On a supposé dans la démonstration que U était connexe, mais le fait d'être analytique étant une propriété locale, on peut généraliser l'énoncé précédent et affirmer que tout fonction holomorphe sur un ouvert U quelconque est analytique sur U.
On remarque aussi que, en donnant une expression aux coefficients du développement de f, cette formule explicite les dérivées n-ièmes de f en a:
-
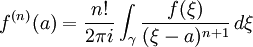
Démonstration de la formule
La preuve de cette formule est assez simple: pour la montrer en un z0 donné il suffit d'appliquer le théorème intégral de Cauchy à la fonction g ainsi définie :
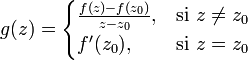
Autres conséquences
Cette formule a de nombreuses applications, outre le fait de montrer que toute fonction holomorphe est analytique, et permet notamment de montrer le principe du maximum et le théorème des résidus.