Construction des entiers naturels - Définition

Il existe plusieurs méthodes classiques de construction des entiers naturels mais celle des entiers de von Neumann est souvent regardée comme la plus simple.

Méthode de von Neuman

Partant de la théorie des ensembles, on identifie 0 à l'ensemble vide, puis on construit le successeur d'un entier naturel comme l'ensemble des entiers naturels qui le précèdent. Plus précisément, les entiers naturels sont construits à partir des règles suivantes :

1. L'ensemble vide est un entier naturel noté 0.
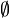
2. Si N est un entier naturel, l'ensemble N U {N} est aussi un entier naturel, appelé le successeur immédiat de N.
3. Tout entier naturel est construit à partir des règles 1 et 2.

Par exemple, le successeur immédiat de 0 est : 0 U {0} = {0} = 1

Celui de 1: 1 U {1} = {0} U {1} = {0,1} = 2

Celui de 2: 2 U {2} = {0,1} U {2} = {0,1,2} = 3

L'axiome de l'infini est nécessaire pour assurer l'existence d'un ensemble contenant tous les entiers naturels. L'intersection de tous les ensembles de ce type (contenant 0 et clos pour l'opération successeur) est alors l'ensemble des entiers naturels. On peut vérifier que ce dernier satisfait les axiomes de Peano.