Axiomes de Peano - Définition

Introduction

Les axiomes de Peano sont, en mathématiques, un ensemble d'axiomes de second ordre proposés par Giuseppe Peano pour définir l'arithmétique.

Axiomes

La définition axiomatique des entiers naturels de Peano est usuellement décrite informellement par cinq axiomes :

1. l'élément appelé zéro et noté 0, est un entier naturel.
2. Tout entier naturel n a un unique successeur, noté s(n) ou Sn.
3. Aucun entier naturel n'a 0 pour successeur.
4. Deux entiers naturels ayant même successeur sont égaux.
5. Si un ensemble d'entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est égal à .

Le premier axiome permet de poser que l'ensemble des entiers naturels n'est pas vide, le troisième qu'il possède un premier élément et le cinquième qu'il vérifie le principe de récurrence.

De façon plus formelle, dire d'un triplet qu'il satisfait à ces axiomes, c'est dire qu'il satisfait aux propriétés suivantes :

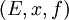
1. E est un ensemble, x est un élément de E, f est une application de E dans lui-même.
2. 
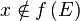
3. f est injective
4. Tout sous-ensemble F de E contenant x et stable par f (c'est-à-dire que ) est égal à E.

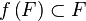
Une telle structure est appelée structure de Dedekind-Peano (d'après le mathématicien Richard Dedekind).

On remarquera que la formulation de la propriété 4 qui contient une quantification sur les ensembles est typiquement du second ordre.

Existence et unicité

L'existence d'une structure de Dedekind-Peano peut être établie par une construction très usuelle dans le cadre de la théorie des ensembles :

• On pose 0 = ∅.
• On définit la « fonction » (au sens intuitif) successeur s en posant, pour tout ensemble a,

.

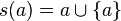
On remarque que pour tous ensembles a et b :

s(a) ≠ 0 ;   s(a) = s(b) ⇒ a = b.

L'ensemble N est l'intersection de tous les ensembles auxquels 0 appartient, et qui sont clos par successeur ; A est clos par successeur, quand pour tout a élément de A, son successeur s(a) est encore élément de A. Pour que cette définition soit correcte, il faut qu'il existe au moins un tel ensemble, ce qui est assuré par l'axiome de l'infini.

la structure (N, 0, s_N), où s_N est la restriction de s à N, satisfait alors les axiomes pré-cités. On peut définir N comme l'ensemble des entiers naturels.

Cet ensemble est aussi l'ensemble des ordinaux de von Neumann finis. Cette construction de N n'est pas vraiment canonique, l'essentiel est que 0 ne soit jamais un successeur et que le successeur soit injectif sur l'ensemble obtenu, mais elle permet de construire de façon simple et uniforme un ensemble représentant chaque cardinalité finie (l'entier n ainsi construit a, en tant qu'ensemble, pour cardinal n), l'axiome de l'infini permettant de prouver qu'ils forment un ensemble.

Deux structures de Dedekind-Peano (X,a,f) et (Y,b,g) sont dites isomorphes s'il existe une bijection ϕ de X dans Y telle que ϕ(a) = ϕ(b) et ϕ o f = g o ϕ. On peut montrer que toutes les structures de Dedekind-Peano sont isomorphes.

Arithmétique de Peano

L'arithmétique de Peano est la restriction des axiomes de Peano au langage de l'arithmétique du premier ordre . Les variables du langage désignent des objets du domaine d'interprétation, ici des entiers. Dans ce langage du premier ordre, on ne dispose pas de variables pour les ensembles d'entiers, et on ne peut quantifier sur ces ensembles. On ne peut donc pas exprimer directement la récurrence par un énoncé tel que celui du paragraphe précédent (« tout sous-ensemble … »). On considère alors qu'un sous-ensemble de est exprimé par une propriété de ses éléments, propriété que l'on écrit dans le langage de l'arithmétique.

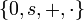
Les axiomes de Peano deviennent alors les 7 axiomes suivants, auxquels s'ajoute, pour la récurrence, un schéma d'axiomes, qui représente une infinité dénombrable d'axiomes (un axiome pour chaque formule du langage) :

1. 
2. 
3. 
4. 
5. 
6. 
7. 
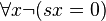
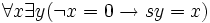
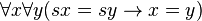
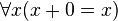
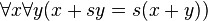
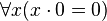
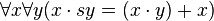
8. Pour toute formule à n + 1 variables libres,

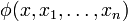
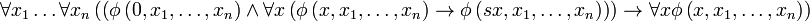
Le schéma d'axiomes exprime bien la récurrence : dans la formule , les variables sont des paramètres, que l'on peut remplacer par des entiers arbitraires . L'axiome pour la formule devient, appliqué à  :

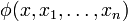
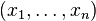
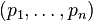
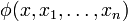
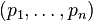
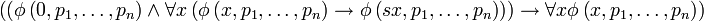
Ce qui exprime bien que, si l'ensemble contient 0, et s'il contient le successeur de chacun de ses éléments, c'est .

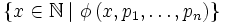
Cependant, le schéma d'axiomes ne donne plus cette propriété que pour les sous-ensembles de qui se définissent dans le langage de l'arithmétique du premier ordre : une infinité dénombrable de sous-ensembles de .

On peut montrer que l'arithmétique de Peano ne peut être finiment axiomatisée, à moins de modifier le langage. Cela n'a donc pas forcément grand sens de chercher à minimiser les axiomes. On peut tout de même remarquer que l'axiome 2 pourrait être éliminé. Il se démontre par récurrence, une récurrence assez singulière, puisqu'il faut bien distinguer le cas 0 du cas successeur, mais que dans ce dernier cas, l'hypothèse de récurrence n'est pas utile.