Vocabulaire élémentaire des probabilités - Définition

Comme tous les langages de spécialistes, le langage des probabilités utilise un vocabulaire spécifique souvent constitué de mots courants auxquels on donne un sens très précis.

Univers

Lors d'une expérience aléatoire, c'est-à-dire soumise au hasard (de alea (latin) le hasard, les dés), on commence par faire l'inventaire de tous les résultats possibles. L'ensemble de tous les résultats possibles sera appelé l' univers Ω des possibles.

Eventualité

Chaque résultat possible sera appelé une éventualité ω.

Exemple: On lance une pièce. L'univers des possibles est Ω={P; F}. Le P est une éventualité de ce lancé.

Exemple 2 : On choisit au hasard un réel strictement compris entre 0 et 1. L'univers des possibles est Ω=]0 ; 1[. le nombre est une des éventualités.

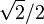
Événement

Un ensemble de résultats possibles définit un événement. C'est un sous-ensemble de l'univers Ω. Il peut être décrit en extension (dans le cas d'un ensemble fini) ou par une description.

Exemple 1: On lance un dé. L'univers est Ω={1 ; 2 ; 3 ; 4 ; 5 ; 6}. La partie A = {1 ; 2 ; 3} est un événement décrit en extension. Cet événement se décrit par la phrase " on obtient au plus 3 en lançant le dé ". Tout lancer de dé donnant comme résultat 1, 2 ou 3 réalise l'événement A.

Exemple 2: Dans le choix d'un nombre au hasard entre 0 et 1, l'événement " on obtient un nombre rationnel " correspond à l'ensemble .

Événement particulier

L'univers Ω est appelé événement certain. Dans un lancer de dé, l'événement " obtenir un numero compris entre 1 et 6 " correspond à l'événement {1 ; 2 ; 3 ; 4 ; 5 ; 6}, c'est-à-dire à l'événement certain.

L'ensemble vide Ø est appelé événement impossible. dans un lancer de dé, l'événement " obtenir plus de 7 " correspond à l'événement {} = Ø, c'est-à-dire l'événement impossible.

Un événement qui ne comporte qu'un seul élément ou éventualité est appelé événement élémentaire.

Opération sur les événements

L'union: l'événement est réalisé dès que A ou B est réalisé. Dans un lancer de dé, si l'événement A est " obtenir un nombre pair " et l'événement B " obtenir un multiple de 3 ", l'événement est l'événement " obtenir un nombre pair OU un multiple de 3 ", c'est-à-dire {2 ; 3 ; 4 ; 6}.

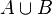
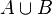
L'intersection: l'événement est réalisé dès que A et B sont réalisés dans la même expérience. Dans un lancer de dé, si l'événement A est " obtenir un nombre pair " et l'événement B " obtenir un multiple de 3 ", l'événement est l'événement " obtenir un nombre pair ET multiple de 3 ", c'est-à-dire {6}.

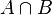
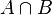
Le contraire: l'événement contraire de A, noté contient tous les éléments de Ω qui ne sont pas dans A. C'est l'événement qui est réalisé dès que A n'est pas réalisé. Dans un lancer de dé, si l'événement A est " obtenir un nombre pair ", l'événement contraire de A, est l'événement " obtenir un nombre impair ".

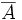
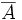
Événements incompatibles

Lorsque deux événements ont une intersection vide, c'est qu'il ne peuvent pas être réalisés au cours d'une même expérience. On les appelle alors événements incompatibles. Dans un lancer de dé, si l'événement A est " obtenir un multiple de 4 " et l'événement B " obtenir un multiple de 3 ", les événements A et B sont incompatibles.

Il ne faut pas confondre les événements incompatibles (qui ne peuvent se produire lors d'une même expérience) et événements indépendants (qui se produisent indépendamment l'un de l'autre).

Maintenant que tout le vocabulaire est en place, il s'agit de quantifier la probabilité de réalisation de chaque événement. C'est l'objet de la création d'une probabilité.