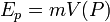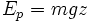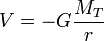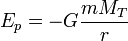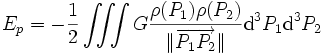Énergie potentielle gravitationnelle - Définition

L'énergie potentielle gravitationnelle (ou énergie gravitationnelle) est le travail nécessaire pour transporter une masse depuis l'infini jusqu'à sa position finale.

Définition

Considérant une masse ponctuelle (exprimée en kg) placée en un point , si on appelle le potentiel gravitationnel dans lequel se déplace cette masse, alors, l'énergie potentielle gravitationnelle (exprimée en joules) de celle-ci vaut

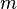
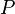
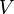
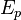
Elle est définie à une constante près. Si la distribution de sources à l'origine du potentiel est d'étendue limitée alors on peut choisir une valeur nulle pour le potentiel à l'infini ce qu'on a supposé dans la précédente formule.

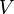
Cas du champ gravitationnel terrestre

Si on considère par exemple un objet soumis au champ gravitationnel de la Terre et qu'on choisit le niveau de la mer comme origine des potentiels alors cette énergie vaut

Avec l'accélération de la gravité terrestre, et l'altitude exprimée en mètres. Notons que cette formule n'est valable que pour de faibles altitudes pour lesquelles peut être considérée effectivement constante.

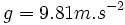
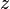
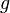
Dans le cas d'un satellite artificiel, comme l'altitude est élevée il faut revenir à la définition et le potentiel gravitationnel suit la loi

où est la constante de gravitation, est la masse de la Terre et est la distance par rapport au centre de la Terre. Alors l'énergie potentielle vaut

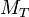
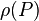
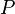
Dans le cas le plus général d'une distribution continue de matière décrite par une densité de masse où est un point quelconque de l'espace, l'énergie potentielle gravitationnelle du système est donnée par la somme de tous les travaux nécessaires pour amener chacune de ses parties depuis l'infini jusqu'à leur position finale.