Aberrations en optique des particules chargées - Définition

Introduction

Les Aberrations en optique des particules chargées sont l'équivalent des aberrations en optique photonique. L'étude des aberrations des lentilles électroniques est presque aussi vieille que le microscope électronique lui-même. Il n'y a pas de différences entre les aberrations géométriques de l'optique photonique ou de l'optique des particules chargées. L'aberration chromatique est assez proche dans les deux disciplines, mais la longueur d'onde de l'optique photonique est remplacée par la variation relative d'énergie. Du fait que l'existence de la charge électrique, certaines aberrations seront la conséquence de la répulsion coulombienne et seront appelées aberrations de charge d'espace pour certaines d'entre elles et aberrations coulombiennes stochastiques pour d'autres.

Ce qu'on appelle l'optique électronique est une restriction de l'optique des particules chargées au cas des électrons. Chaque fois que la masse n'intervient pas dans la description d'une aberration il est cependant courant de la décrire comme s'il s'agissait d'un électron.

Historique

Les premiers calculs des coefficients d'aberration ont été effectués dès le début des années 1930 par Scherzer qui utilisait la méthode des trajectoires paraxiales et par Glaser qui a introduit la méthode de l'eikonal. Pendant les années 1930, les aberrations des lentilles circulaires sont étudiées intensivement et plusieurs auteurs aboutissent à des formules concernant les différents coefficients d'aberrations. Notamment Scherzer parvient à démontrer un théorème particulièrement intéressant pour la résolution des microscopes électroniques: Quel que soit le dessin d'une lentille, électrostatique ou magnétique, son aberration sphérique est toujours positive.

Dans les années 1940, des auteurs parmi lesquels on retrouve Scherzer, calculent les aberrations des quadrupoles et proposent un certain nombre de méthodes pour annuler leur aberration sphérique.

C'est à la fin des années 1940 que des auteurs commencent à adresser le problème des aberrations du seconds ordre dans des dispositifs courbes tels que le secteur magnétique ou le secteur électrostatique: Pour les secteurs magnétiques, Hintenberger en 1948, puis Kerwin, Tasman, Boerboom et finalement Enge en 1967. Pour les secteurs électrostatiques, Ewald et Liebl en 1957, Wollnick en 1965.

Définition canonique des aberrations

Dans un très grand nombre de systèmes d'optique électronique ou ionique, il est possible de privilégier une trajectoire médiane, paramétrée en z, distance le long de la trajectoire et une tension d'accélération nominale E. La trajectoire médiane est généralement l'axe de symétrie mécanique des instruments que l'on appellera axe principal. Certaines parties de cet axe sont droites, mais d'autres parties peuvent être courbes, par exemple, dans les secteurs électrostatiques ou magnétiques utilisés dans les spectromètres de masse. On peut alors considérer n'importe quel système optique comme une fonction de transformation des trajectoires entre un plan d'entrée situé à z_i, où l'indice "i" signifie « input » et un plan de sortie situé à z_o, où l'indice "o" signifie « output ». Ces indices sont un peu malheureux, car ils entraînent une confusion avec « image » et « objet », mais c'est ainsi qu'ils sont définis dans la littérature.

Dans un plan donné, perpendiculaire à l'axe principal, repéré par des axes OX et OY, n'importe quelle trajectoire électronique ou ionique peut être caractérisée par un vecteur (x, y, a, b, m, e) où

• (x,y) sont les coordonnées de la particule
• (a, b) sont les angles d'ouvertures respectifs par rapport à l'axe principal OZ dans les plans ZOX et ZOY
• e=dE/E est la différence relative entre la tension d'accélération de la particule et la tension d'accélération nominale E .
• m=dM/M est la différence relative entre la masse de la particule et la masse nominale M.

Chaque composante du vecteur de sortie peut alors s'exprimer comme une fonction des composantes du vecteur d'entrée et peut être approximé par une Série de Taylor.

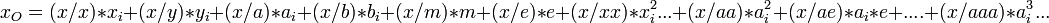
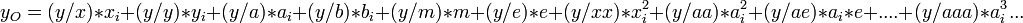
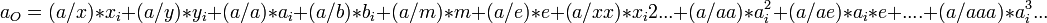
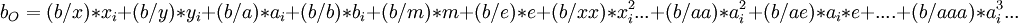
Il doit être clair que (x/ae) ou (a/x) ou y(bbb) désignent des coefficients. L'ensemble complet de ces coefficients est parfois appelé la Matrice de Transfert. Il faut comprendre que dans la mesure où on l'on connait les coefficients de chaque constituant du système, il est possible de calculer facilement les coefficients de l'ensemble du système.

On peut donner à chaque coefficient une signification physique. Par exemple (x/x) et (y/y) sont des grandissements alors que (a/x) et (b/y) sont des inverses de distance focale. On peut aussi signaler que (x/m) est un coefficient de dispersion en masse et (x/e) un coefficient de dispersion en énergie.

Dans un certain nombre de cas particuliers, on peut démontrer que certains coefficients sont nécessairement nuls pour des raisons de symétrie. Par exemple, une lentille électrostatique pourvue d'une symétrie de révolution aura ses coefficients du second ordre (a/xx), (a/yy), (a/xy) etc... égaux à zéro.

Les termes du deuxième et du troisième ordre (et bien sûr, au-delà) sont considérés comme des effets parasites, non désirés, dans la plupart des systèmes optiques. On les appelle des « aberrations ». Certains dispositifs, par exemple des hexapoles, qui produisent un certain type d'aberrations - dans le cas des hexapoles, ce sont des aberrations du deuxième ordre, sont inclus dans des systèmes optiques en vue d'annuler des aberrations produits par d'autres dispositifs indispensables dans l'instrumentation considérée? Par exemple, les secteurs magnétiques qui sont utilisés pour leur dispersion en masse, produisent également des termes parasites (x/aa), (x/ae)...