Accélération - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Applications - Accélération de la convergence en mathématiques - Accélération en mécanique

Introduction

L'accélération désigne couramment une augmentation de la vitesse ; en physique, plus précisément en cinématique, l'accélération est une grandeur vectorielle qui indique la modification affectant la vitesse d'un mouvement en fonction du temps.

Dans le langage courant, l'accélération s'oppose à la décélération et indique l'augmentation de la vitesse de l'évolution d'un processus quelconque, par exemple l'accélération du rythme cardiaque ou l'accélération des évènements d'une actualité.

Applications

Dans la vie courante, on distingue trois événements que le physicien regroupe sous le seul concept d'accélération :

aller plus vite (accélérer au sens commun plus restrictif) : l'accélération est positive, c'est-à-dire que le vecteur accélération possède une composante dans le sens de la vitesse
aller moins vite (freiner ou décélérer ou ralentir dans le langage commun) : l'accélération est négative, ou le vecteur accélération possède une composante opposée au sens de la vitesse
changer de direction (tourner ou virer dans le langage commun) : l'accélération comporte une composante perpendiculaire à la vitesse, si celle-ci change de direction sans changer de norme.

La notion d'accélération est formalisée par Pierre Varignon (1654-1722) le 20 janvier 1700, comme un écart infiniment petit de vitesse $d v$ sur le temps infiniment petit $d t$ mis pour modifier cette vitesse. Réitérant l'approche qu'il avait utilisé deux ans plus tôt pour définir la notion de vitesse, il utilise le formalisme du calcul différentiel mis au point quelques années plus tôt par Leibniz (1646-1716).

Calcul de la distance parcourue

Par exemple, vous souhaitez calculer la distance parcourue par un solide en mouvement accéléré, dans le cas où l'accélération $a$ est constante. Dans la formule ci-dessous, $d 0$ représente le déplacement initial, $v 0$ la vitesse initiale, $Δ t$ la durée du trajet et $a$ l'accélération :

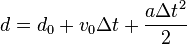
$d = d_{0}+v_{0} {\Delta t} + \frac{a{\Delta t}^2}{2}$

Exemple

Afin de déterminer la hauteur d'un pont, on lâche une pierre depuis le haut dudit pont. Celle-ci met la durée secondes pour atteindre le sol. Quelle est la distance parcourue ?

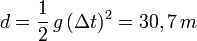
Sachant que a=g=9,81 m.s^-2, la distance parcourue est $d = \frac{1}{2}\,g\, (\Delta t)^2 = 30,7\, m$

==== Implémentation ==== (il ya des fautes !!)

L'implémentation (en C) ci dessous montre comment déterminer la vitesse et la distance instantanée en fonction de l'accélération, de la vitesse initiale et de la distance initiale. Le code ci-dessous reprend l'exemple précédent en affichant la vitesse instantanée et la distance parcourue en fonction du temps toutes les 0.5 secondes (période d'échantillonnage). Lors de la lecture d'un signal, on utilise une fenêtre d'échantillonnage la plus faible possible.

      #include              #define square(x) ((x) * (x))             int main(int argc, char* argv[])      {      	double accel = 9.81;    // m/s²      	double speed = 0.0;     // m/s      	double position = 0.0;  // m             	double dt = 0.5;        // frequence d'echantillonage en secondes             	double time = 0.0;      	while (1) //Boucle      	{      		// Termine au bout de 2.5 secondes      		if (time > 2.5) break;             		printf("%05.2f - %05.2f - %05.2f\n", time, speed, position);             		position = (accel * square(dt) / 2.0) + speed * dt + position;      		speed += accel * dt;             		time += dt;      	}                    	return 0;      }

Accélération de la convergence en mathématiques

Le terme est aussi utilisé en mathématiques, par exemple l'accélération de la convergence d'une suite (par des procédés comme le Delta-2 d'Aitken) signifie que l'écart entre la valeur des éléments de la suite et sa limite est plus petit que pour la suite initiale à un rang n donné.