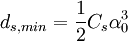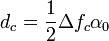Aberrations en optique des particules chargées - Définition

Les aberrations dans les systèmes à symétrie de révolution

Aberrations géométriques du troisième ordre

Dans un système à symétrie de révolution, c'est-à-dire un système constitué de lentilles électrostatiques et de lentilles magnétiques comme le sont les microscopes électroniques, il est naturel de travailler en coordonnées cylindriques en exprimant la position de la particule à l'aide de son rayon vecteur r et de son azimut φ. On travaillera alors avec les variables complexes u et v et w définis par

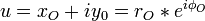
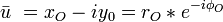
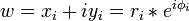
La symétrie de révolution conduit à éliminer les termes d'ordre pair, à commencer par le second ordre. Elle impose aussi, pour tous les termes du toisième ordre de type , à ne conserver que ceux dont la phase est φ:

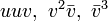
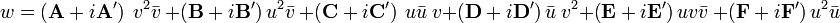
Par ailleurs Par des considérations de symétrie, et en vertu du théorème de Malus Dupin qui impose:

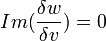
on arrive à simplifier et à supprimer un certain nombre de termes:

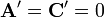
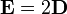
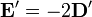
Ce qui conduit à une relation valide aussi bien pour les lentilles magnétiques que pour les lentilles électrostatiques

Mais dans le cas des lentilles électrostatiques, on peut mettre à profit le fait qu'aucune force ne peut amener un électron à quitter un plan méridien.

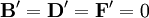
A est connu comme le coefficient d'aberration sphérique
D est connu comme le coefficient de coma
D est connu comme le coefficient de coma anisotropique
B est connu comme le coefficient d'astigmatisme
B' est connu comme le coefficient d'astigmatisme anisotropique
C est connu comme le coefficient de courbure de champ
F est connu comme le coefficient de distorsion
F' est connu comme le coefficient de distorsion anisotropique

Toutes ces sont discutées ci-dessous

Discussion détaillée des différentes aberrations géométriques

On peut définir de façon canonique 5 types d'aberrations géométriques: l'aberration sphérique, coma, la courbure de champ, l'astigmatisme et la distorsion.

Aberration sphérique

Réprésentation de l'aberration sphérique.

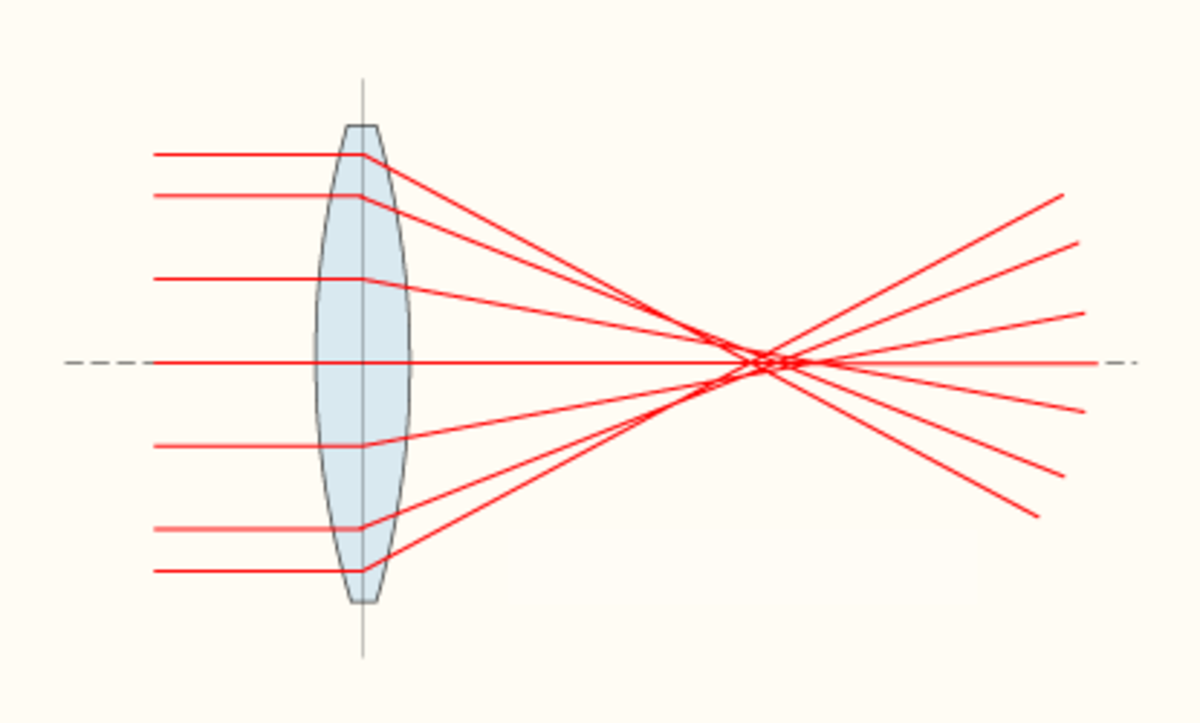
L'aberration sphérique est une aberration du troisième ordre qui traduit le fait qu'une lentille, qu'elle soit magnétique ou électrostatique, est toujours plus convergente pour les trajectoires périphériques que pour les trajectoires centrales. Le coefficient d'aberration sphérique C_s est défini par la relation:

r_s = C_sθ³M

où r_s est la distance à l'axe, dans le plan image de Gauss de la trajectoire associé à l'angle d'ouverture θ et M étant le grandissement du système optique considéré.

La section du faisceau n'est pas minimale au plan de Gauss, mais à un plan voisin. Dans ce plan, la section du faisceau est appelée disque de moindre confusion d_s,min dont on peut montrer qu'il est égal à: Pour un faisceau ayant un angle d'ouverture α₀, le faisceau n'est pas focalisé en un point, mais en un disque dans le plan image, appelé disque de moindre confusion de diamètre minimum d_s,min :

α₀, étant l'angle d'ouverture du faisceau.

Scherzer a démontré par un théorème qui porte son nom que l'aberration sphérique était toujours positive dans un système à symétrie de révolution. On a cependant imaginé à la fin des années soixante-dix de contourner le théorème se Scherzer par des systèmes qui ne sont pas à symétrie de révolution et qui nécessitent de faire passer le faisceau hors d'axe. Ces systèmes consistent en un certain nombres d'étages de multipoles. Leur réglage nécessitant des algorithmes sophistiqués, ce n'est que depuis le début des années 2000 qu'ils ont pu être intégrés dans des microscopes électroniques commercialisés.

Astigmatisme

L'astigmatisme a pour effet de ne pas faire converger les rayons issus d'un même point suivant leurs directions initiales. En considérant une focale F_m suivant le plan méridien, et l'autre F_s suivant le plan sagittal, on observe une différence de focale Δf_a = F_m − F_a. De cette différence résulte un cercle de moindre confusion de diamètre d_a donné par :

d_a = Δf_aα₀

Dans le cas d'une lentille, l'origine de cette aberration vient des variations de champs dues aux inhomogénéités de la lentille ou des contaminations éventuelles sur la surfaces des diaphragmes et de l'échantillon. L'astigmatisme est corrigé par une paire de stigmateurs, décalés de 45°.

Aberrations chromatiques

En pratique, le faisceau électronique n'est pas complètement monochromatique, c'est-à-dire que la longueur d'onde (ou l'énergie) varie faiblement d'un électron à l'autre. La focalisation des lentilles magnétiques magnétique dépendant fortement de l'énergie des électrons, il en résulte une succession de foyers qui sont compris entre le foyer pour les électrons les plus lents F_l et celui pour les plus rapides F_r. Cette différence Δf_c = F_l − F_r et la constante d'aberration chromatique caractérise le cercle de moindre confusion dont le diamètre d_c est donnée par :

Cette aberration est dite d'ordre un, car elle est proportionnelle à l'ouverture angulaire α₀.