Albert Girard - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Biographie - Œuvres - Travaux

Travaux

La nouvelle invention en algèbre.

Quoique l'on compte peu de publications chez Girard et que son algèbre n'ait pas la richesse de l'algèbre nouvelle de Viète (sauf indication expresse du contraire, les équations de Girard sont numériques), Girard occupe une place importante dans l'histoire des mathématiques. Il connaît Viète et fait plusieurs emprunts à son analyse spécieuse ; il l'enrichit, excellant dans l'art de la Syncrèse du mathématicien des Parthenay ; il y décèle des erreurs. Enfin, donnant un sens aux quantités négatives, il est le premier à énoncer (sans le démontrer), le théorème fondamental de l'algèbre.

Girard écrit en 1629 dans son "Invention nouvelle en l'Algèbre" :

« Toutes les équations d'algèbre reçoivent autant de solutions que la dénomination de la plus haute quantité le démontre. »

et quelques autres identités concernant les polynomes symétriques. Ces relations, que Newton retrouva par la suite, indépendamment et qui permettent de calculer, grâce aux formules de Viète, les sommes des puissances de toutes les racines d'un polynôme à l'aide de ses seuls coefficients, seront complétées définitivement par Leonhard Euler, Gauss et Edward Waring.

Un progrès dans les notations.

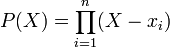
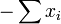
Girard introduit dans ce même ouvrage l'emploi des parenthèses et des crochets, qui est restée, et des notations moins heureuses, qui n'ont pas été retenues. Sa nomenclature algébrique est parfois très originale. Girard nomme en effet du nom surprenant de "meslés" les monômes intervenant dans le développement d'un polynôme ( $P(X)=\prod_{i=1}^n(X- x_i)$ ) et nombres du premier ( $-\sum x_i$ ), du second (

∑	x_ix_j
i < j

), du troisième meslés, etc, leurs coefficients. De même il désigne par le mot de "factions" les polynômes symétriques des racines...

On notera toutefois que, pour Girard, les nombres complexes ne sont pas comme chez Descartes des imaginaires, mais des inexplicables avec lesquels il n'hésite pas à travailler.

La géométrie sphérique

On doit encore à Girard un traité de trigonométrie (édité en 1626) et la traduction des travaux de Stevin (1625). D'après Michel Chasles, Girard est au nombre des géomètres qui, à l'imitation de Viète, ont été à l'initiative des transformations des triangles sphériques. Un an avant Snellius, il englobe les quatre triangles formés par les arcs de cercle qui ont pour pôles les trois sommets d'un triangle donné sous le nom collectif de triangle réciproque ; ainsi, il regarde comme réciproques d'un triangle donné, à la fois le triangle de Viète et celui de Snellius.

Il fut également l'inventeur (concomitamment avec William Oughtred) des symboles "sin, cos et tan". Dans son traité de Trigonométrie, qui est à la suite d'une table des sinus, tangentes et sécantes, il montre par sa préface qu'il s'était occupé à restaurer l'Analyse géométrique des Anciens, et a rétabli les traités dont les titres nous ont été transmis par Pappus ; il dit, à ce sujet, qu'après ce petit Traité de Trigonométrie, « qu'il donne comme échantillon, il mettra au jour quelque chose de plus grand. » La mort l'en a empêché. Dans la préface ) sa traduction des œuvres de Stevin, (éditée en 1625), il annonce également son intention de restaurer les Pôrismes d'Euclide, mais cet ouvrage, prêt à paraître, n'aura pas vu le jour et s'est perdu.

Autres travaux

Enfin, Girard est le premier qui ait indiqué l'aire du triangle sphérique rectangle. Cette découvert, énoncée par Harriot en 1603 n'avait pas été encore publiée par les anglais. Il est également le premier à donner l'expression générale de la formation des suites de Fibonacci.