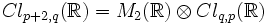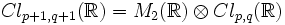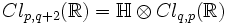Algèbre de Clifford - Définition
La liste des auteurs de cet article est disponible ici.
Structure des algèbres de Clifford
Dans cette partie, nous supposons que l'espace vectoriel V est de dimension finie et que la forme bilinéaire de Q est non-dégénérée. Une algèbre centrale simple sur K est une algèbre de matrices sur une algèbre de division (de dimension finie) avec un centre K. Par exemple, les algèbres centrales simples sur les réels sont les algèbres de matrices sur soit les réels, soit les quaternions.
- Si V possède une dimension paire, alors
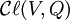
- Si V possède une dimension paire, alors
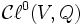
- Si V possède une dimension impaire, alors
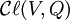
- Si V possède une dimension impaire, alors
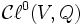
La structure des algèbres de Clifford peut être établie explicitement en utilisant le résultat suivant. Supposons que U possède une dimension paire et une forme bilinéaire non-singulière avec un discriminant d, et supposons que V est un autre espace vectoriel avec une forme quadratique. L'algèbre de Clifford de U+V est isomorphe au produit tensoriel des algèbres de Clifford de U et
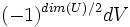
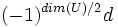
Ces formules peuvent être utilisées pour trouver la structure de toutes les algèbres de Clifford réelles;
Spineurs
Supposons que p+q=2n est pair. Alors l'algèbre de Clifford
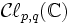
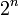
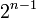
Si p+q=2n+1 est impair alors l'algèbre de Clifford
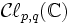
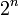
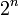
Plus généralement, les groupes de spin et les groupes de pin sur tout corps ont des représentations similaires dont la structure exacte dépend de la structure des algèbres de Clifford correspondantes : toutes les fois qu'une algèbre de Clifford possède un facteur qui est une algèbre de matrice sur certaines algèbre de division, nous obtenons une représentation correspondante des groupes de spin et de pin sur cette algèbre de division. Pour des exemples sur les réels :
Spin et groupes de Pin
Dans cette partie, nous supposons que V est de dimension finie et sa forme bilinéaire non-singulière. (Si K est de caractéristique 2, ceci implique que la dimension de V est pair).
Le groupe de Pin PinV(K) est le sous-groupe du groupe de Clifford
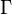
Rapellons, à partir de la partie précédente, qu'il existe un homomorphisme à partir du groupe de Clifford sur le groupe orthogonal. Nous définissons le groupe spécial orthogonal comme étant l'image de
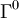
Il existe un homomorphisme à partir du groupe de Pin vers le groupe orthogonal. L'image est constituée des éléments de norme de spin 1 ∈ K*/K*2. Le noyau est constitué des éléments +1 et -1, et est d'ordre 2 à moins que K soit de caractéristique 2. De manière similaire, il existe un homomorphisme à partir du groupe de Spin vers le groupe spécial orthogonal de V.
Dans le cas courant, lorsque V est un espace défini positif ou négatif sur les réels, le groupe de spin s'applique sur le groupe spécial orthogonal, et est simplement connexe lorsque V est de dimension au moins égale à 3. Attention : Ceci n'est pas vrai en général : si V est
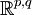
Voir groupe spineur, spineur.