Application (mathématiques) - Définition

Ensemble des applications entre deux ensembles

L'ensemble des applications de E dans F est souvent noté F^E. Quand E et F sont des ensembles finis, si on note |E| le cardinal d'un ensemble E, on a :

|F^E| = |F|^|E|.

Il s'agit également de l'ensemble des familles indexées par E d'éléments de F, et on peut utiliser également cette notation :

.

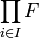
Dans le cas dégénéré, où E est l'ensemble vide, le produit cartésien de E par F est vide, il y a une seule application dans F^∅, celle dont le graphe est l'ensemble vide.

Dans l'autre cas dégénéré où F est vide mais E non vide, alors l'unique sous ensemble de , l'ensemble vide, ne définit pas d'application : l'existence d'une image pour tout élément de E ne pourra jamais être vérifiée. Donc ∅^E = ∅ si E ≠ ∅.

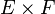
Définition

La définition usuelle en mathématiques d'une fonction est donc ensembliste et présuppose essentiellement celle de couple et de produit cartésien. Une application ou fonction est un triplet f = (E, F, G) avec G ⊂ E × F, et qui vérifie que pour tout x de E il existe un unique y de F tel que le couple (x, y) appartienne à G. L'ordre des ensembles du triplet est arbitraire et on trouve d'ailleurs des variations suivant les ouvrages. On décompose souvent la propriété caractéristique en deux clauses :

Existence. ∀ x ∈ E ∃ y ∈ F   (x, y) ∈ G ;

Unicité. ∀ x ∈ E ∀ y ∈ F ∀ y’ ∈ F ( [ (x, y) ∈ G et (x, y’) ∈ G] ⇒ y = y’ ).

En d'autres termes ceci signifie que G intersecte chaque sous-ensemble {x} × F, en un unique point, dont l'existence est donnée par la première clause, et l'unicité par la seconde. Ce point, élément de F, est appelé image de x par l'application f et noté f(x). Pour bien distinguer l'image d'un élément de E, qui est un élément de F, de l'image de f, qui est un sous-ensemble de F, on parle parfois dans ce dernier cas d’ensemble image de f.

On dit également que f associe à x l'élément f(x), ou encore que f envoie x sur f(x). Les formes passives « x est envoyé par f sur f(x) », « f(x) est associé à x par f » sont aussi utilisées.

Si x, élément de E, vérifie f(x)=y, on dit que x est un antécédent de y. Un élément y de F peut très bien avoir plusieurs antécédents ou n'en avoir aucun.

Pour une fonction de E dans F qui à x associe f(x) on note :

par exemple pour la fonction de la variable réelle qui à un nombre associe son carré :

Dans l'exemple précédent on a utilisé la structure des réels pour définir la fonction. Pour un ensemble E quelconque on peut toujours définir l’identité ou application identique, qui associe à tout élément x de E l'élément x lui-même. Son graphe est la diagonale du produit cartésien , le sous-ensemble défini par la relation x=y.

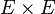
Si F est non vide, alors on peut associer à tout élément b de F, une application dite application constante de E dans F, qui associe à tout élément de E l'élément b. Son graphe est donc E × {b}.

On utilise parfois d'autres terminologies et d'autres notations. Les fonctions définies sur l'ensemble N des entiers naturels (ou une partie de celui-ci) sont souvent appelées suites, par exemple les suites réelles sont les fonctions de N dans l'ensemble R des réels. On utilise alors la notation indicielle : (u_n)_{n ∈ N} désigne la suite, écriture qui peut être abrégée en (u_n), et u_n désigne l'image par cette suite de l'entier n.

Cette notation s'étend aux familles, indexées par I d'éléments d'un ensemble F donné, qui sont, avec une autre notation et une autre terminologie, des fonctions de I dans F.