Application (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
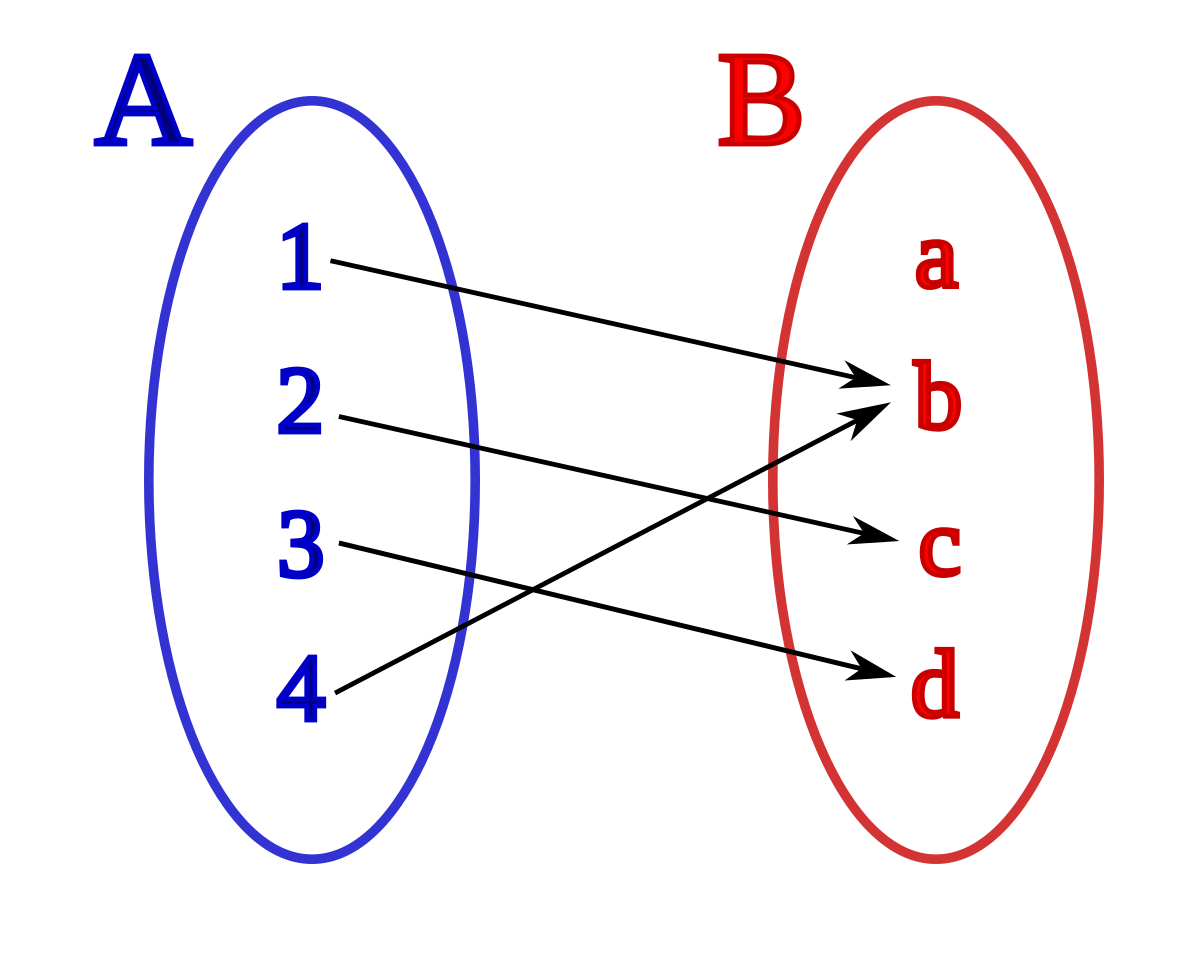
En mathématiques, une application est une relation entre deux ensembles pour laquelle chaque élément du premier (appelé ensemble de départ ou source) est relié à un unique élément du second (l’ensemble d'arrivée ou but). Le terme est concurrencé par celui de fonction, bien que ce dernier désigne parfois plus spécifiquement les applications entre ensembles de nombres ou englobe au contraire plus largement les relations pour lesquelles chaque élément de l'ensemble de départ est relié à au plus un élément de l'ensemble d'arrivée.
Une application est donc un objet issu de la théorie des ensembles, défini par son graphe et associé aux notions d'image et d'antécédent. Elle peut être injective ou surjective selon l'unicité ou l'existence d'un antécédent pour chaque élément de l'ensemble d'arrivée. La conjonction de ces deux propriétés définit une bijection, qui admet alors une application réciproque. Les applications peuvent aussi être composées ou restreintes à un sous-ensemble de leur ensemble de départ.
En dehors du contexte de l'analyse, le terme est spécifié entre autres en géométrie affine, en algèbre linéaire, en topologie et dans la théorie des systèmes dynamiques. Il est parfois remplacé par celui d'opérateur ou de morphisme, voire de flèche, notamment en théorie des catégories.
Fonction et application
La notion de fonction en tant que correspondance entre deux types d'objet est relativement ancienne. Mais le terme n'apparait qu'à la fin du XVIIe siècle sous la plume de Leibniz en 1694, il s'agit alors de fonction associée à une courbe géométrique : Leibniz dit ainsi que l'abscisse, l'ordonnée ou le rayon de courbure d'une courbe en un point M est une fonction du point M. Dans la même époque, Newton parle de fluente pour des quantités dépendant d'une variable qu'il appelle le temps (tout en précisant que le rôle joué par le temps, peut l'être par une autre quantité). La notation sous la forme f ne s'est pas mise en place tout de suite. Jean Bernoulli propose d'appeler X la fonction de x, Leibniz invente une notation permettant de travailler sur plusieurs fonctions différentes :
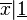
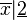
Parallèlement se développe, en géométrie, la notion d'application pour des correspondances ponctuelles.
Dans les années 1950, l'école Bourbaki tente de faire correspondre les deux notions en parlant de
- relation ou graphe fonctionnel : (E,F,G) où E et F sont deux ensembles non vides et où G est un sous-ensemble non vide de E x F vérifiant en outre, pour tous couples (x,y) et (x’,y’) de G, si x = x’ alors y = y’. (i.e. chaque élément de E possède au plus une image) ;
- application pour un graphe fonctionnel dans lequel tout élément de E possède exactement une image.
S'appuyant sur cet avis, les mathématiques modernes des années 1970 distinguent alors deux objets différents
- la fonction : définie par un ensemble de départ E, un ensemble d'arrivée F et une relation de E vers F dans laquelle chaque élément de E possède au plus une image. L'ensemble des éléments de E possédant une image est alors appelé domaine de définition de la fonction
- l'application : définie par un ensemble de départ E, un ensemble d'arrivée F et une relation de E vers F dans laquelle chaque élément de E possède une image et une seule
En pratique, le fait qu'il suffise de réduire l'ensemble de départ d'une fonction à son ensemble de définition pour la transformer en application rend peu utile ce distinguo. Celui-ci n'a d'ailleurs jamais été adopté par la communauté mathématique dans son ensemble, qui continue à utiliser ces deux termes dans leur sens historique, le terme fonction étant utilisé comme synonyme du terme application dans le cas particulier où l'ensemble d'arrivée est