Application (mathématiques) - Définition

Application réciproque

• Si une application f : E → F est bijective, à tout élément de F est associé un unique antécédent par f dans E. Ceci définit donc une application, que l'on appelle application réciproque de f, et qui, dans ce cas, est également une bijection, dite aussi bijection réciproque de f.

On la note f ^{− 1}. Son graphe est le symétrique du graphe de f, c'est-à-dire que si G est le graphe de f, le graphe de f ^{− 1} est {(y, x) | (x, y) ∈ G}. Dans le cas où E = F = R, l'ensemble des nombres réels, le graphe de f ^{− 1} est, dans le plan R², le symétrique de celui de f par rapport à la première bissectrice. Ainsi la fonction des réels positifs dans eux-mêmes qui à x associe x² est une bijection, sa réciproque est la racine carrée, et un graphe de l'une se déduit d l'autre par symétrie par rapport à la droite d'équation y=x.

Dans le cas par exemple d'une fonction numérique, quand on peut parler de l'inverse d'un élément a de F, celui-ci peut s'écrire a^-1. Dans ce cas f(x) ^{− 1} désigne l'inverse de l'élément f(x). Il s'agit de la fonction inverse 1/f (si elle existe). La notation f ^{− 1} est réservée à la bijection réciproque de f (si elle existe).

• L'application f : E F est injective, si et seulement s'il existe une surjection g: F → E réciproque à gauche de f, c'est-à-dire que g o f est l'identité de E. Quand f est injective, il suffit de prendre pour g une application qui à un élément de l'image de f associe son antécédent par f, et qui est définie arbitrairement sur les autres éléments. Cette fonction n'est pas unique, sauf si f est également bijective. La réciproque découle directement de ce que g est une application.

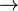
• L'application f : E F est surjective, si et seulement s'il existe une injection g: F → E réciproque à droite de f, c'est-à-dire que f o g est l'identité de F. Supposons f surjective, dans le cas où l'ensemble image de f est infini, l'existence de cette injection repose en toute généralité sur l'axiome du choix (énoncé pour toute surjection, c'est même équivalent à l'axiome du choix). L'application g est en effet une fonction de choix sur l'ensemble des ensembles des antécédents d'un élément de F, elle choisit bien un antécédent pour chaque élément de F. Cette fonction n'est pas unique, sauf si f est également bijective (cas où, l'antécédent étant unique, l'axiome du choix n'est pas nécessaire). L'existence d'une fonction g réciproque à droite de f fournit bien directement un antécédent par f pour chaque élément de F.

Théorie des ensembles

La notion de fonction n'est pas primitive dans les théories des ensembles de Zermelo ou de Zermelo-Fraenkel, et se définit grâce aux notions de couple et de produit cartésien, qui ne sont pas non plus primitives. La notion peut se développer dans la théorie de Zermelo (sans l'axiome de l'infini), avec l'axiome d'extensionnalité, l'axiome de la paire, l'axiome de la réunion, l'axiome de l'ensemble des parties et le schéma d'axiomes de compréhension. On a eu besoin en une occasion, pour montrer en toute généralité l'existence d'une réciproque à droite d'une fonction surjective, de l'axiome du choix.

Il arrive souvent en théorie des ensembles qu'une fonction soit identifiée à ce que l'on a appelé précédemment son graphe. C'est-à-dire qu'une fonction est définie comme un ensemble de couples vérifiant les propriétés d'existence et d'unicité de l'image, dont on vérifie facilement qu'elles ne mettent pas véritablement en jeu les ensembles de départ et d'arrivée, c'est-à-dire qu'avec cette définition, G est une fonction quand c'est un ensemble de couples vérifiant la propriété d'unicité :

Unicité. ∀ x ∀ y ∀ y’ ( [ (x, y) ∈ G et (x, y’) ∈ G] ⇒ y = y’ ).

L'ensemble de départ de la fonction est l'ensemble des premières projections de G, qui se définit par compréhension, tout comme l'image de la fonction qui est l'ensemble des secondes projections de G (voir l'article produit cartésien pour des détails dépendant de la représentation des couples). Il n'y a plus d'ensemble d'arrivée intrinsèque, c'est-à-dire que f est une fonction de E dans F devient une propriété de f : E est l'ensemble des premières projections de f, et l'ensemble image, ensemble des secondes projections, est inclus dans F. L'injectivité est une propriété qui ne dépend que du graphe de la fonction. Par contre, dans ce contexte, la surjectivité ou la bijectivité deviennent une propriété de f et de l'ensemble d'arrivée choisi (f est surjective de E dans F).

On peut avoir à s'intéresser aux classes fonctionnelles, qui sont des classes de couples vérifiant les deux propriétés indiquées en début de paragraphe, mais portant sur une classe au lieu de l'ensemble G. Le schéma d'axiomes de remplacement, qui complète la théorie des ensembles de Zermelo pour donner celle de Zermelo-Fraenkel, énonce que l'image d'un ensemble par une classe fonctionnelle, est un ensemble, et donc cette classe fonctionnelle est une fonction (comme ensemble de couples).