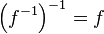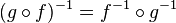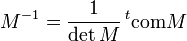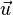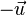Application réciproque - Définition

Résultats généraux

Définition

La réciproque de la fonction ƒ de X vers Y, est la fonction ƒ^–1 qui de Y retourne versX.

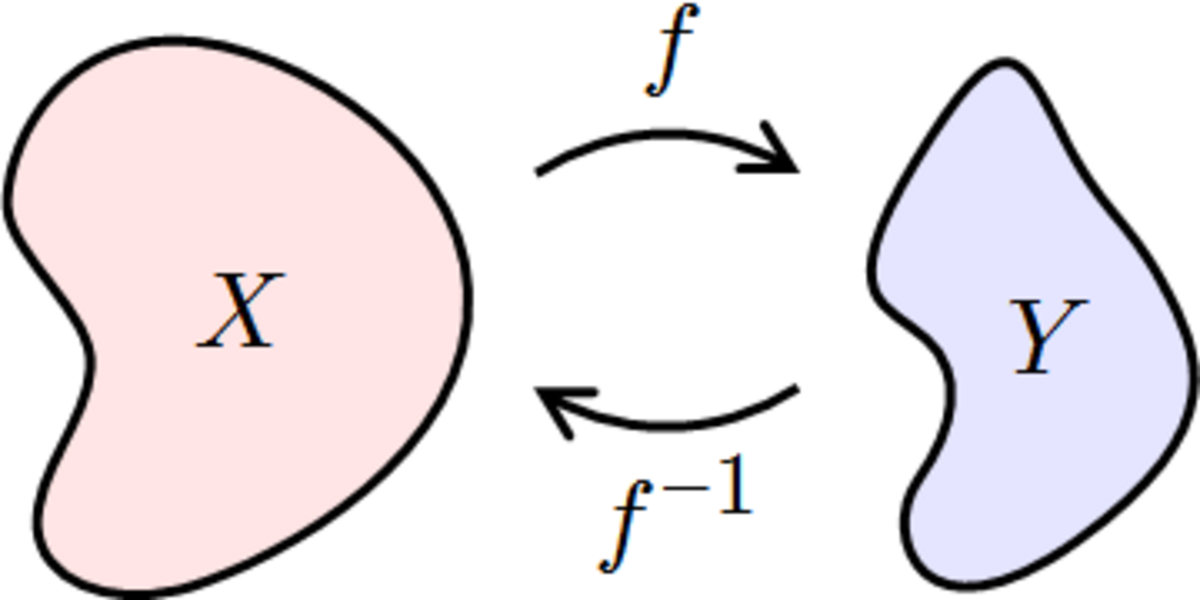
Si f est une application d'un ensemble X vers un ensemble Y et s'il existe une application g de Y vers X telle que :

et ,

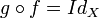
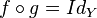
on appelle g l'application réciproque de f et on la note f ^{− 1} .

L'existence d'une telle fonction g n'est possible que si f est bijective :

1. chaque élément de l'ensemble d'arrivée doit être atteint par f car
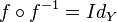
2. chaque élément de l'ensemble d'arrivée doit être atteint une seule fois par f car si f(a)=f(b) alors et a = b.

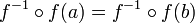
Une telle application g est alors unique : c'est l'application qui, à tout élément y de Y, associe l'unique antécédent de y par f.

Propriétés

Réciproque de la réciproque

La double propriété : et montre que f est aussi l'application réciproque de f ^{− 1}, c'est-à-dire que

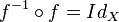
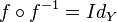
Réciproque d'une composée

l'inverse de g ƒ est ƒ^–1 g^–1

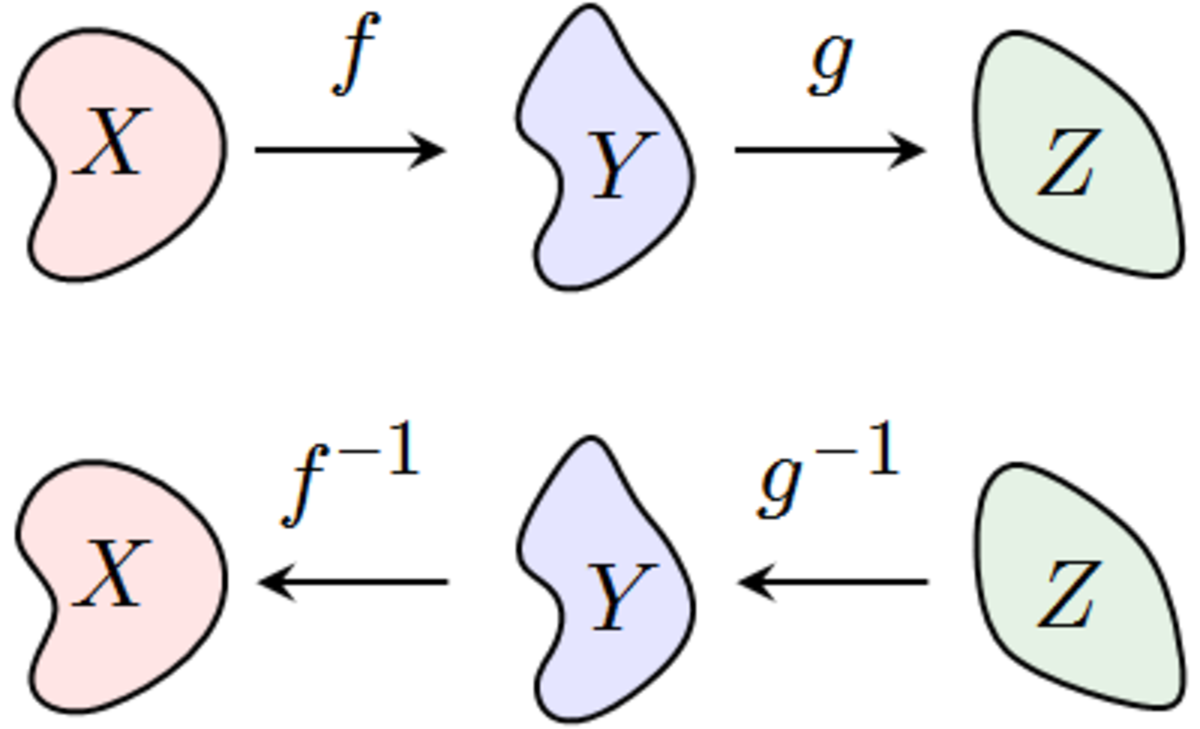
La réciproque de la composée de deux fonction est donné par la formule

Il faut remarquer que l'ordre de ƒ et g a été inversé; pour défaire ƒ suivi de g, il faut d'abord défaire g puis défaire ƒ.

Involution

Certaines application de E vers E sont leur propre réciproque, c'est le cas par exemple de

 :

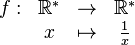
ou de toute symétrie orthogonale dans le plan.

De telles applications sont dites involutives.

Généralisation

Lorsque la fonction f n'est pas bijective, il est possible de définir une relation réciproque définie sur qui à tout élément de f(X) associe ses antécédents par f. Si f n'est pas injective, la relation créée n'est pas une application, on parle alors de réciproque multiforme. Si f est injective, la relation ainsi créée est bien l'application réciproque de f restreinte à l'ensemble d'arrivée f(X).

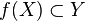
Pour certaines fonctions f non surjectives, il existe une fonction g telle que . Il suffit pour cela que f soit injective. On dit alors que g est un inverse à gauche pour f.

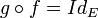
Pour certaines fonctions f non injectives, il existe une fonction g telles que . Il suffit pour cela que f soit surjective (en admettant l'axiome du choix).

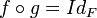
Réciproque en algèbre linéaire

En algèbre linéaire un morphisme de groupe, d'anneau, de corps, d'espace vectoriel bijectif admet une application réciproque qui est aussi un morphisme de même type. L'application et sa réciproque sont appelés des isomorphismes.

Dans le cas d'une application f linéaire d'un espace vectoriel E vers un espace vectoriel F, tous deux de dimension finie. f admet une application réciproque si et seulement si E et F ont même dimension et si la matrice M de f dans les bases (B₁,B₂) est inversible. La réciproque de f possède alors pour matrice dans la base (B₂,B₁) la matrice note M ^{− 1} appelée matrice inverse de M et valant

où det (M) est le déterminant de la matrice M et où ^tcomM est la transposée de la comatrice de M

Exemple de réciproque de transformation du plan

Les transformations du plans sont les applications bijectives du plan, il est donc intéressant d'en connaitre les réciproques, du moins pour les transformations de références

Transformation	Transformation réciproque
Translation de vecteur	Translation de vecteur
Symétrie de centre O ou d'axe (d)	Symétrie de centre O ou d'axe (d)
Homothétie de centre C et de rapport k	Homothétie de centre C et de rapport 1/k
Rotation de centre C et d'angle θ	Rotation de centre C et d'angle - θ
Similitude directe de centre C, de rapport k et d'angle θ	Similitude directe de centre C, de rapport 1/k et d'angle - θ
Similitude indirecte de centre C, de rapport k et d'axe (d);	Similitude indirecte de centre C, de rapport 1/k et d'axe (d);
symétrie glissée d'axe (d) et de vecteur	symétrie glissée d'axe (d) et de vecteur
affinité d'axe (d) de direction (d') et de rapport k	affinité d'axe (d) de direction (d') et de rapport 1/k