Calcul des séquents - Définition

Discussion

Le calcul des séquents et les autres formalismes logiques

Le calcul des séquents, contrairement aux systèmes à la Hilbert ou à la déduction naturelle, n'est pas un formalisme très intuitif ; le propos de Gentzen était de résoudre certains problèmes techniques rencontrés en déduction naturelle lors de la démonstration de la cohérence de l'arithmétique. C'est pourquoi le calcul des séquents doit se penser comme un formalisme pour raisonner sur les preuves formelles plutôt que pour rédiger des preuves formelles, ce à quoi la déduction naturelle est plus adaptée. On peut toutefois facilement montrer que toute formule prouvable dans l'un des systèmes l'est également dans l'autre.

L'intérêt du calcul des séquents est de rendre explicite un grand nombre de propriétés de la logique :

• la dualité hypothèse/conclusion exprimée par la symétrie parfaite entre la droite et la gauche dans les séquents ;
• la symétrie de la logique classique exprimée par le partitionnement des règles en gauche et droite ;
• les propriétés structurelles (commutativité, idempotence) exprimées par les règles du groupe structurel.

La règle de coupure

La règle de coupure est une généralisation du modus-ponens. Pour le voir il faut considérer le cas particulier de la règle où :

• Γ, Δ et Γ' sont des séquences vides de formules ;
• Δ' contient une unique formule B.

Dans ce cas particulier les deux séquents prémisse de la règle deviennent respectivement et tandis que le séquent conclusion devient .

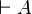
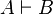
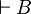
La règle de coupure joue un rôle très particulier dans le calcul des séquents pour deux raisons :

• elle est indispensable pour formaliser les preuves mathématiques ; en effet l'expérience montre que, à l'exception des démonstrations faciles de tautologies, la moindre preuve de mathématique utilise quasiment exclusivement la règle de coupure ;
• plus techniquement, c'est la seule règle à violer la propriété de la sous-formule ; si on observe les règles du calcul des séquents on voit que pour chaque règle, sauf la coupure, les formules apparaissant dans les séquents prémisse sont encore présentes dans le séquent conclusion. Autrement dit, si une démonstration du calcul des séquents n'utilise pas la règle de coupure, alors toutes les formules apparaissant dedans sont des sous-formules du séquent conclusion, c’est-à-dire que le séquent conclusion de la démonstration est le plus compliqué de toute la démonstration.

La propriété de la sous-formule était très importante pour Gentzen car c'est elle qui permet de démontrer la cohérence du calcul : en effet le séquent le plus simple possible est le séquent vide qui ne contient aucune formule ni à gauche, ni à droite. Or ce séquent exprime une contradiction. Pour voir que le calcul est cohérent il suffit donc de voir que le séquent vide n'est pas prouvable ; mais une démonstration sans coupure du séquent vide ne devrait contenir que des séquents plus simples, et il n'y en a aucun. Donc toute démonstration du séquent vide doit utiliser la règle de coupure. Et voilà comment Gentzen a été conduit à démontrer son célèbre théorème d'élimination des coupures qui stipule justement que de toute démonstration d'un séquent, on peut extraire une démonstration sans coupure du même séquent, ce qui montre en corollaire qu'il n'existe aucune démonstration du séquent vide. C'est en adaptant cette démonstration d'élimination des coupures au cas de l'arithmétique que Gentzen a produit sa preuve de cohérence de l'arithmétique.