Caractère d'une représentation d'un groupe fini - Définition

Introduction

En mathématiques le caractère d'une représentation d'un groupes finis est un outil utilisé pour analyser les représentations d'un groupe fini.

Le caractère d'une représentation (V, ρ) d'un groupe G correspond à l'application de G dans le corps de l'espace de la représentation qui à un élément s associe la trace de l'image de s par ρ.

Cette définition n'est pas compatible avec celle des caractères d'un groupe en général qui ne prend ses valeurs que dans l'ensemble des complexes différents de zéro.

L'utilisation du caractère d'une représentation d'un groupe fini est essentielle pour la classification des représentations. La somme directe de représentation possède pour caractère la somme des caractère et deux représentations irréductibles différentes possèdent des caractères orthogonaux.

Définitions

• Le caractère χ_ρ de la représentation (V, ρ) est une application de G un groupe fini dans K le corps de la représentation qui à s associe la trace de ρ_s.

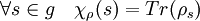
Un cas important correspond à celui où le corps K est égal à celui des nombres complexes.

Un exemple simple correspond au cas des représentations de dimension un. Il est alors possible d'identifier V à K. Le caractère apparaît comme un morphisme de groupe. Le théorème de Lagrange démontre que l'ensemble des images est inclus dans celui des racines g-ième de l'unité.

• Un caractère irréductible est le caractère d'une représentation irréductible.

Premières propriétés

• L'image de l'unité par un caractère est égale à la dimension n de V.

Cette propriété provient du fait que ρ₁ est égal à l'identité de V.

• Si s et t sont deux éléments du groupe, alors st et ts ont même image par le caractère.

Cette propriété est une conséquence directe des propriétés de la trace : deux matrices semblables (c’est-à-dire qui représentent le même endomorphismes dans deux bases différentes ont même caractères).

• Si deux représentations sont isomorphes alors elles ont même caractère.

Cette propriété se démontre comme la propriété précédente.

• Si s et t sont deux éléments conjugués du groupe, c’est-à-dire s'il existe un élément u tel que usu^-1 = t, alors ils ont même image par le caractère.

La trace est invariante par changement de base. Si la matrice associée à ρ_u est considérée comme une matrice de passage, on constate que les images de s et t par ρ ont des matrices associées semblables.

• Si le corps K est inclus dans celui des complexes et s un élément du groupe, alors l'image de s^-1 par le caractère est le conjugué de l'image de s.

L'endomorphisme ρ_s possède comme polynôme annulateur X^g - 1 d'après le théorème de Lagrange. Son polynôme minimal est scindé, car le corps est algébriquement clos et séparable c’est-à-dire qu'il n'admet pas de racine multiple (cf polynôme cyclotomique). En conséquence l'endomorphisme est diagonalisable. Chaque valeur propre λ est une racine de l'unité et admet pour inverse sa valeur conjuguée. En conséquence l'image par ρ de s^-1, égal à l'inverse de ρ_s et est diagonalisée dans la même base avec pour valeur sur la diagonale les conjuguées de celle de ρ_s, ce qui démontre la proposition. Ces propriétés ne sont pas spécifiques aux caractère fini des groupes. On obtient le corollaire suivant :

• Si le corps K est inclus dans celui des réels et s un élément du groupe, alors l'image de s^-1 par le caractère est la même que celle de s.

Cette propriété se généralise au cas où le corps est de caractéristique finie p s'il est algébrique. La théorie de Galois démontre l'existence d'un automorphisme φ de corps laissant stable l'extension de dimension deux du corps premier F_p (cf corps fini). L'application φ joue le rôle d'application conjuguée. φ² est égale à l'identité et si x est un élément de K, x.φ(x) est un élément du corps premier (celui engendré par 1). Si λ est une racine g-ième de l'unité alors λ.φ(λ) est un élément du corps premier dont la puissance g est égal à un. Comme g est premier avec p, la caractéristique du corps, λ.φ(λ) est égal à un et φ(λ) est égal à λ_-1. En conséquence l'image de s^-1 par le caractère est égal à φ(χ_s).