Caractère d'une représentation d'un groupe fini - Définition

Orthogonalité

Lemme de Schur

Le théorème de Maschke donne une importance particulière aux représentations irréductibles. En effet, toute représentations est somme directe de représentations irréductibles.

Soit deux représentations irréductibles (V₁, ρ¹) (V₂, ρ²) de caractères respectifs χ₁ et χ₂. Les caractères sont des éléments de l'espace vectoriel C des applications de G dans K. Soient M¹ = (m¹_ij) et M² = (m²_kl) les représentations sous forme matricielles de ρ¹ et ρ². On dispose des relations suivantes :

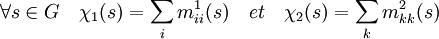
En vue d'appliquer le corollaire 4 du lemme de Schur il est nécessaire de supposer que le corps K est de caractéristique soit nulle soit première avec g l'ordre du groupe et que le polynôme X^g - 1 est scindé dans K. On dispose alors des deux propriétés suivantes :

• (1) Si les représentations ρ¹ et ρ² ne sont pas isomorphes, alors :

• (2) Si les deux représentations sont isomorphes, alors :

Où δ_ij désigne le symbole de Kronecker. Les démonstrations sont données dans l'article associé.

Caractéristique nulle

On suppose que le corps K est de caractéristique nulle et que le polynôme X^g - 1 est scindé dans K. Alors si l'on définit le produit hermitien suivant :

• Le produit hermitien canonique < | > de l'espace C des fonctions du groupe G à valeur dans K est donnée par la formule suivante :

Ici, si a est un élément de K a^* désigne le conjugué de a. La définition permet d'exprimer la proposition suivante :

• Si χ₁ et χ₂ sont deux caractères irréductibles, soit les représentations associées sont isomorphes et <χ₁ | χ₂> = 1, soit elles ne le sont pas et <χ₁ | χ₂> = 0.

On peut exprimer cette dernière proposition par :

• La famille des caractères irréductibles est orthonormale.

En effet, l'expression du produit hermitien prend la forme suivante :

La dernière égalité provient du fait que le caractère d'un inverse est le conjugué d'un caractère (cf Premières propriétés). En terme matricielle cette égalité se traduit par :

Le corollaire 4 du lemme de Schur permet de conclure.

Exemple

Il n'existe qu'un unique groupe simple d'ordre 168, il n'est pas abélien et correspond au deuxième groupe simple non commutatif, si ces groupes sont ordonnés à l'aide de leur ordre. On trouve la table suivante, établie dans l'article détaillé :

Car. irr. C1 C2 C3 C4 C7a C7b χ1 1 1 1 1 1 1 χ3a 3 -1 0 1 1/2.(-1 + i√7) 1/2.(-1 - i√7) χ3b 3 -1 0 1 1/2.(-1 - i√7) 1/2.(-1 + i√7) χ6 6 2 0 0 -1 -1 χ7 7 -1 1 -1 0 0 χ8 8 0 -1 0 1 1

Les cardinaux des classes de conjugaisons sont C₁ : 1, C₂ : 21, C₃ : 56, C₄ : 42, C_7a : 24, C_7b : 24. On en déduit le produit hermitien pour deux caractères χ_φ et χ_ψ, dans le cas d'une représentation complexe :

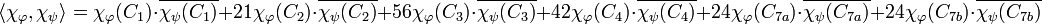
Les caractères de la table sont bien tous de norme 1 et orthogonaux deux à deux.

Conséquences

Cette propriété d'orthogonalité entraine des conséquences théoriques immédiates :

• Soient (V, ρ) une représentation d'un groupe fini G, (V_i) une décomposition de V en sous-espaces irréductibles et (W, σ) une représentation irréductible de G. La représentation ρ_i désigne la restriction de ρ à V_i, χ désigne le caractère de ρ et ψ celui de σ. Le nombre de sous-espaces V_j de la famille (V_i) tel que (V_j, ρ_j) soit isomorphe à (W, σ) est égal à <χ|ψ>.

En effet, il suffit de remarquer que le caractère d'une somme directe est égal à la somme des caractères. L'orthogonalité des représentations irréductibles permet de conclure.

On en déduit les corollaires suivants :

• La norme d'un caractère par le produit hermitien canonique est égale à un entier.

• Un caractère est irréductible si et seulement si sa norme par le produit hermitien canonique est égal à un.

Représentation régulière

Il existe une représentation qui possède toutes représentations irréductibles comme sous-représentations, elle est appelée représentation régulière. Le théorème de Cayley montre que le groupe G est isomorphe à un sous-groupe du groupe symétrique d'ordre g. Si V est un K espace vectoriel de dimension G, il est possible d'indexer une base B de V par G. Le groupe G opère transitivement sur B. L'unique prolongement linéaire de l'action de groupe à V est une représentation, elle est dite régulière. C'est une représentation de degré g égal à l'ordre du groupe. Elle vérifie la propriété suivante :

• La représentation régulière (V, ρ) de G est fidèle.

C’est-à-dire qu'elle est injective (cf théorie des représentations d'un groupe fini).

Sous réserve que les caractères irréductibles forment une famille orthonormale de K^G, alors si (W, σ) est une représentation irréductible de G de degré d :

• Il existe exactement d sous-espaces invariants W_i de V, d'intersection nulle deux à deux, tel que la restriction de ρ, la représentation régulière, à W_i soit isomorphe à (W, σ).

Cette décomposition n'est pas unique. Le nombre de sous-espaces isomorphes à W de V est en général supérieur à d, mais ils ne sont pas en somme directe. Il existe néanmoins une unique décomposition de la représentation régulière.

• Il existe un unique sous-espace maximal S_W de V contentant tous les sous-espaces isomorphe à W. Il est appelé composante isotypique de W dans V. Les composantes isotypiques sont en somme directe égal à V.

Sous reserve des mêmes hypothèses que précédemment, si (W_j, σ_j) est l'ensemble des représentations irréductibles de G quand j varie de 1 à h, alors l'égalité suivante est vérifiée :

• Soit d_j le degré de la représentation irréductible (W_j, σ_j) et g l'ordre de groupe, alors :

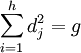
Les démonstrations sont données dans l'article associé.

Ces propriétés sont utilisées, par exemple pour établir la table des caractères du groupe alterné d'indice 4 et 5, ou encore du groupe simple d'ordre 168.

Fonction centrale

Une fonction centrale est une application constante sur chaque classe de conjugaison du groupe. Les premières propriétés des caractères montrent que ce sont des fonctions centrales. Dans le cas où ils forment une famille orthonormale, alors :

• Les caractères irréductibles forment une base orthonormale de l'espace vectoriel des fonctions centrales à valeur dans K.

On en déduit que :

• Si h désigne le nombre de classes de conjugaison de G alors il existe h représentations irréductibles distinctes à un isomorphisme près.