Caractère d'une représentation d'un groupe fini - Définition
La liste des auteurs de cet article est disponible ici.
Contexte
Histoire
Les travaux de Jordan avec la publication d'un livre sur les équations algébriques représente une première analyse d'un groupe fini de matrices représentant un groupe de Galois. Frobenius démarre en 1896 l'étude de la théorie des caractères des groupes finis, les caractères ne sont pas encore liés à la notion de représentation. Cette même année il communique, dans une lettre à Dedekind les caractères des représentations irréductibles des groupes symétriques d'ordre quatre et cinq.
La théorie est rapidement développée, entre 1897 et 1899 la machinerie est mise en place. Frobenius développe le produit tensoriel, les représentations induites ainsi que son théorème de réciprocité. En 1900 il détermine les caractères des groupes symétriques et l'année suivante ceux des groupes alternés.durant cette époque, Heinrich Maschke démontre le théorème portant maintenant son nom qui stipule que toute représentation d'un groupe fini est somme directe de représentations irréductibles.
William Burnside comprend rapidement la profondeur des travaux de Frobenius. Il utilise la théorie des caractères pour montrer qu'un groupe d'ordre pn.qm si p et q sont premiers est un groupe résoluble. Il publie en 1911 la deuxième édition d'un livre de référence. Elle formalise en une théorie le savoir de l'époque sur les groupes finis, l'édition contient les travaux sur les caractères de Frobenius.
Un autre acteur important de la théorie Issai Schur est un élève de Frobenius. Non seulement il travaille sur les aspects théoriques et démontre son lemme, mais de plus, dans l'année 1925 il applique la théorie à la physique quantique.
La théorie est l'objet d'un large développement durant le XXe siècle. On peut citer les travaux d'Artin avec la notion de caractère virtuel, ceux de Richard Brauer avec son théorème sur les combinaisons linéaires à coefficients entiers ou encore plus récemment Thompson qui reçoit la Médaille Fields pour avoir démontré une vieille conjecture de Burnside annonçant que tout groupe fini d'ordre impair est résoluble.
Motivation
Le théorème de Maschke démontre que si un corps K est soit de caractéristique nulle soit première avec l'ordre du groupe G étudié alors toutes représentation sur un K-espace vectoriel est somme directe de sous-espaces irréductibles.
La théorie se concentre alors sur deux points clés : comment connaître les représentations irréductibles et comment, pour une représentation donnée connaître ses facteurs irréductibles. La théorie des caractères répond partiellement à la première des deux questions et totalement à la deuxième.
Introduction par l'exemple
Considérons le polynôme P[X] à coefficients dans les nombres rationnels Q défini par P[X] = X3 + X + 1. La théorie montre qu'il existe un espace vectoriel V sur Q de dimension six et que le groupe de Galois G opére sur V. Plus précisément, G est un groupe d'automorphismes de V isomorphe à S3. La difficulté réside maintenant dans le fait que la dimension de l'espace est égale à six. Le groupe se représente par six matrices carrées 6x6. Ce qui rend le problème plus ardu.
Recherchons dans un premier temps toutes les représentations irréductibles. Il existe un premier cas aisé, celui où V est de dimension un et identifié à C et où le morphisme t associe à tout élément de S3 la valeur un. On parle alors de représentation triviale. Un deuxième cas σ utilise le même espace V, il associe à tout élément de S3 sa signature, c’est-à-dire -1 si la permutation est une transposition et 1 sinon.
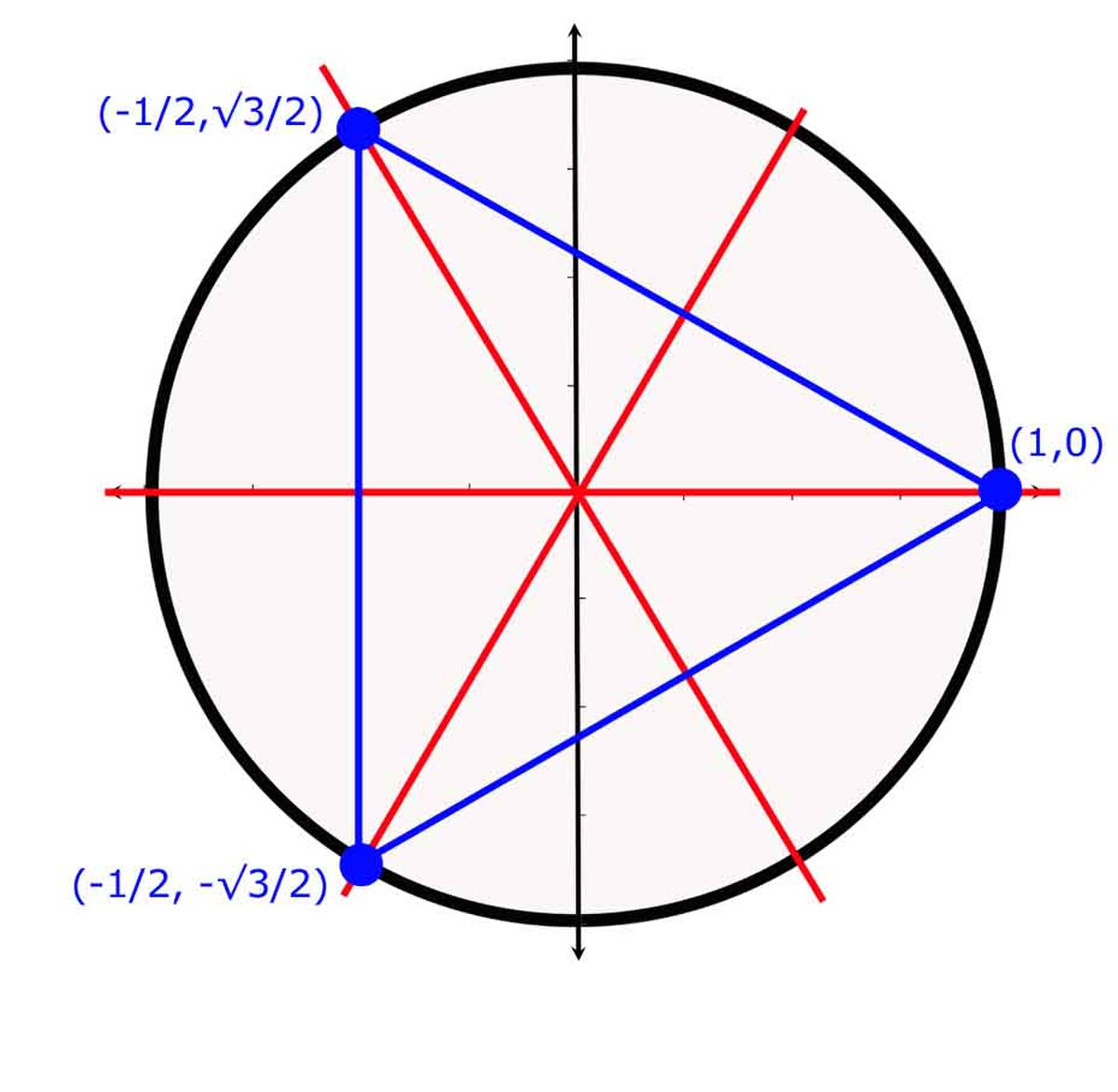
Le troisième cas est illustré sur la figure de gauche. L'espace vectoriel est de dimension deux et le morphisme θ associe aux trois transpositions les symétries orthogonales d'axes ceux représentés en rouge sur la figure. Les deux éléments d'ordre trois sont alors les rotations d'angles 2.π/3 et -2.π/3.
La théorie des caractères montre qu'il n'existe pas d'autre représentation irréductible de ce groupe. Il existe deux manières de s'en rendre compte, soit par la représentation régulière qui montre que l'ordre (ici égal à 6) est égal à la somme des carrés des degrés des différentes représentations irréductibles ici égal à 1 + 1 + 4, soit par les fonctions centrales qui montre que le nombre de représentations irréductibles est égal aux nombre de classes de conjugaison du groupe. Une fonction centrale est une fonction du groupe constante sur les classes de conjugaison.
Remarquons que le groupe S3 comporte trois classes de conjugaison, celle de l'unité, celle des trois transpositions T = {t1, t2, t3} et celle des deux cycles d'ordre trois C = {c1, c2}. Il est relativement simple de vérifier que les trois caractères sont constants sur chaque classe de conjugaison, cette propriété est générale pour tous les caractères. De plus, il existe un produit scalaire (dans le cas général un produit hermitien) tel que les caractères irréductibles forment une base orthonormale. Ce résultat est au coeur de la théorie des caractères. Dans notre cas, si Si φ et ψ sont deux fonctions centrales il est donné par :

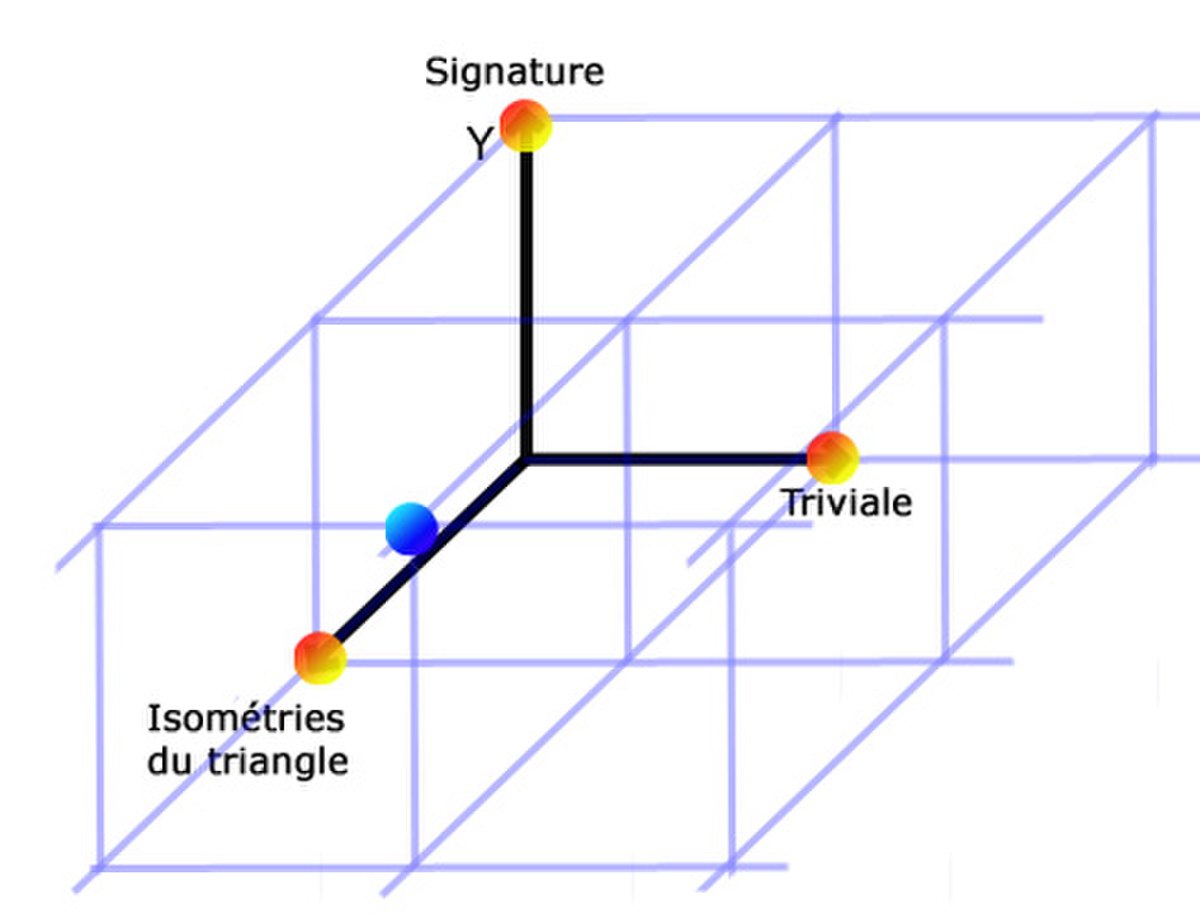
Ces propriétés permettent simplement de factoriser l'exemple donné sur S3. Notons χt,χσ, χθ les caractères des trois représentations irréductibles et χρ le caractère de la représentation du groupe de Galois. Comme, la famille des caractères irréductibles est une base, il existe trois scalaires a, b et c tel que :
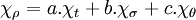
Comme la base est orthonormée, les trois coefficients sont données par les formules :

La figure de droite illustre les caractères du groupe S3. Les caractères représentés par des boules orange sont les trois irréductibles, la boule bleu représente le caractère de la représentation de Galois. Elle est combinaison linaire des trois caractères irréductibles avec les coefficient un pour la triviale, un pour la signature et deux pour celle des isométries du triangle.

















































