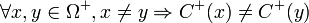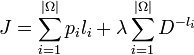Codage entropique - Définition

Propriétés des codes de source

Un code doit respecter certaines propriétés pour être utile: une concaténation de mots de code doit avoir un décodage unique, aisé, et permettre la plus grande compression possible. Certaines conditions sont imposées au code pour satisfaire ces propriétés.

Autrement dit, toute séquence codée est décodable par une unique séquence de symbole de source.

L'intérêt des codes préfixés est qu'ils sont décodables immédiatement, en les parcourant de la gauche vers la droite. La fin d'un mot de code est reconnaissable immédiatement, sans la nécessité d'un code spécial pour indiquer la terminaison ou une séparation. De plus, les codes préfixes sont uniquement décodables.

• Exemple: Soit le code défini par le tableau suivant

Le code C₁ = {0,10,110,111} est un code préfixé. La séquence codée comme

11011111010110010110111

se décompose facilement en:

110 111 110 10 110 0 10 110 111

et se décode donc comme:

c d c b c a b c d

Code optimal

Un code optimal est un code préfixé de longueur moyenne minimale. La compression est d'autant plus forte que la longueur moyenne des mots de code est faible. Trouver un code optimal revient donc à choisir les longueurs des mots de codes, par rapport à la distribution de probabilité des symboles de source, afin de rendre la longueur moyenne minimale. Pour trouver un tel code, il faut minimiser la longueur moyenne du code L(C), sous les conditions de l'inégalité de Kraft, soit:

minimiser sous la condition

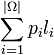
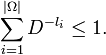
Par la méthode des multiplicateurs de Lagrange, on définit le lagrangien J:

que l'on différentie par rapport aux l_i. Un rapide calcul donne les longueurs optimales , soit une longueur moyenne , c'est-à-dire l'entropie H(X). Les longueurs données par cette méthode ne sont cependant pas entières, sauf dans le cas exceptionnel où les p_i sont des puissance négatives de 2. Ce résultat n'est donc pas utile en pratique, et il est nécessaire d'utiliser d'autres méthodes pour construire un code optimal.

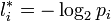
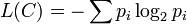
Applications

La principale application du codage entropique est la compression de données. Si le codage de Huffman a rapidement laissé sa place aux méthodes par dictionnaire pour la compression de données génériques, il reste très utilisé en compression d'images, et est présent dans la norme JPEG. Le codage arithmétique s'est montré efficace seulement à partir du début des années 1990, et est utilisé aussi bien en compression de données génériques (PAQ) qu'en compression d'images (JPEG 2000) et vidéo (H.264).

Types de codes

Codage de Shannon-Fano

Le codage de Shannon-Fano est la première méthode de codage entropique efficace, développée en même temps par Claude Shannon et Robert Fano en 1949. Cette méthode n'est en revanche pas optimale, et a été rapidement supplantée par le codage de Huffman.

Codage de Huffman

Le codage de Huffman a été développé par David Huffman en 1952. C'est un code optimal au niveau symbole. De nombreuses améliorations ont été proposées après sa publication, notamment le codage adaptatif, qui permet de ré-estimer les probabilités à la volée. Ceci permet d'effectuer le codage et le décodage sans disposer de la totalité des statistiques de la source.

Codage arithmétique

Le codage arithmétique est une extension du codage de Shannon-Fano-Elias. Il est optimal au niveau bit.

Code universel