Code parfait et code MDS - Définition

Introduction

Un code parfait (ou code MDS, pour maximum distance séparable) est un concept de la théorie des codes et qui traite plus spécifiquement des codes correcteurs.

Un code correcteur est un code permettant au récepteur de détecter ou de corriger des altérations suite à la transmission ou au stockage. Elle est rendue possible grâce à une redondance de l'information. Un code est dit parfait s'il ne contient aucune redondance inutile. Le concept correspond à un critère d'optimalité. Un code est dit MDS s'il vérifie un autre critère d'optimalité s'exprimant dans le contexte des codes linéaires.

Il existe de nombreux codes correcteurs. Les sommes de contrôles sont les exemples les plus simples, on peut citer néanmoins aussi des codes cycliques comme des BCH ou ceux de Reed-Solomon. Les codes parfaits sont plus rares, on peut citer par exemple les codes de Hamming ou les codes de Golay binaire de longueur 23 et ternaire de longueur 11..

Contexte

Code correcteur

Les codes correcteurs ont leur source dans un problème très concret lié à la transmission de données. Dans certains cas, une transmission de données se fait en utilisant une voie de communication qui n'est pas entièrement fiable. Les données, lorsqu'elles circulent sur cette voie, sont susceptible d'être altérées. L'objectif d'un code correcteur est l'apport d'une redondance de l'information de telle manière à ce que l'erreur puisse être détectée ou corrigée.

Rappelons brièvement la formalisation d'un code. Un message est un mot formé de k lettres prises dans un alphabet A, notons E l'ensemble des messages. Ce message est encodé par une application φ injective en un mot contenant n lettres dans un alphabet A' non nécessairement égal à A. Notons q le cardinal de A' et F l'ensemble d'arrivé de φ. F est l'ensemble des mots formé de n lettres pris dans un alphabet à q éléments, F est donc de cardinal qⁿ. L'ensemble φ(E) est inclus dans F et est appelé code et un élément de cet ensemble un mot du code. La longueur du code correspond à k, le nombre de lettres constituant le message. Ces notations sont utilisés dans tout l'article.

Distance de Hamming

hyper-cube binaire de dimension quatre

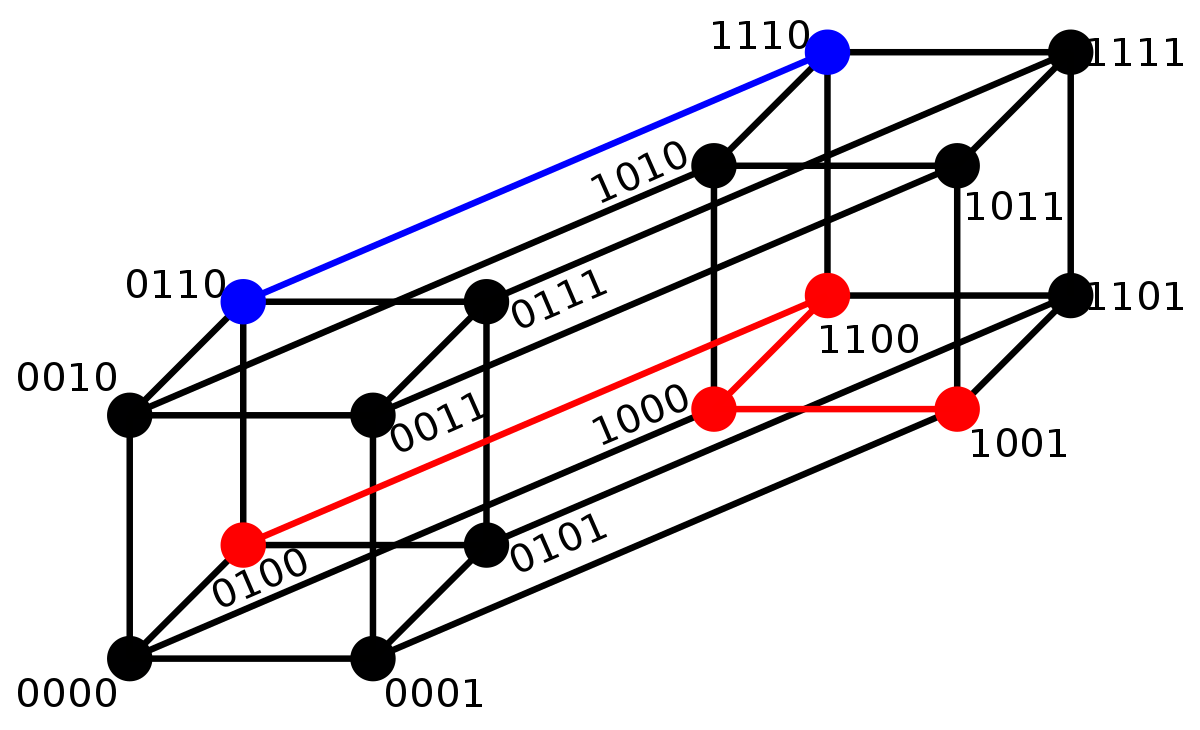
Un concept essentiel dans la théorie des codes correcteurs est celui de la distance de Hamming. À deux mots du code, elle associe le nombre de lettres qui diffèrent.

• La distance de Hamming entre "ramer" et "cases" est 3.

La figure de droite illustre un cas largement répandu dans l'industrie, celui où les lettres de l'alphabet sont binaires. Dans l'exemple choisi, les mots sont composés de quatre lettres. La distance entre 0110 et 1110 est égale à un car il est nécessaire de parcourir un segment du graphique pour joindre les deux mots. On peut aussi remarquer que les deux mots diffèrent seulement par leur première lettre. La même approche montre que la distance entre 0100 et 1001 est égale à trois.

Dans l'exemple de la figure, l'alphabet est un corps fini, il est en effet muni de deux lois : une additive et l'autre multiplicative. Cela confère à l'ensemble une structure d'espace vectoriel. Dans ce cas là, la distance dérive d'une pseudo-norme appelée poids de Hamming et qui associe à un vecteur le nombre de coordonnées non nulles. La distance de Hamming entre deux mots est alors égale au poids de leur différence.

Cas général

Capacité de correction et distance minimale

Une première question apparaissant pour l'analyse d'un code est la valeur et la signification du paramètre t utilisé dans la définition du code parfait. la valeur t correspond au plus grand entier tel que les boules fermées de rayon t et de centre les mots du code ne s'intersectent pas deux à deux:

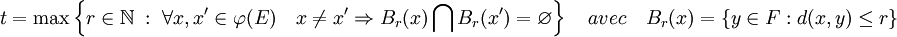
Si δ est la distance minimale entre deux mots du code, l'inégalité triangulaire montre que si t est strictement inférieur à δ/2, alors l'intersection des boules fermées de centres les mots du codes et de rayon t ont une intersection vide. En effet, si m un mot de F était élément de deux boules fermées de centre c et c' et de rayon t alors :

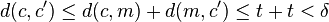
Ce qui implique que c et c' sont égaux par définition de la distance minimale δ.

Réciproquement, montrons que si t est supérieur ou égal à δ/2 alors il existe au moins deux boules fermées de rayon t et de centre deux points du code distincts d'intersection non vide. La fonction distance de Hamming, prend ses valeurs dans un ensemble fini donc le minimum est atteint. Soit c et c' deux mots du code tel que d(c, c') soit égal à δ, où δ désigne la distance minimale. Les deux mots c et c' diffèrent par δ coordonnées. Soit m le mot ayant les mêmes coordonnées que c sauf pour les t premières des δ coordonnées qui diffèrent entre c et c' où m possède les coordonnées de c', m est à une distance de t de c et à une distance inférieure ou égale à t de c', ce qui permet que conclure que:

• La plus grande valeur t tel que les boules fermées de centre les mots du code et de rayon t aient une intersection vide est le plus grand entier strictement inférieur à δ/2.

On remarque de plus, que le plus grand nombre d'erreurs corrigibles de manière certaine est égal à la valeur t. En effet, une erreur n'est corrigible de manière certaine seulement s'il existe un unique mot du code proche du message transmis, ce qui correspond à la définition du paramètre t.

Borne de Hamming

Une approche pour déterminer le nombre de redondances nécessaires à la correction de t erreurs est le dénombrement. Il est possible de calculer le cardinal de l'espace F, celui d'une boule fermée de rayon t pour la distance de Hamming et donc le nombre maximal de messages transmissibles par le code avec une capacité de correction de t erreurs.

L'espace F est formé par des mots de n lettres pris dans un alphabet contenant d lettres. Il contient donc d ⁿ éléments.

Calculons le nombre de points à une distance de Hamming i d'un point c donnée. L'ensemble des points à une distance de i de c est celui contenant les mots ayant i coordonnées différentes de c. À chaque point de l'ensemble correspond un sous-ensemble de i éléments choisi parmi n. Le nombre d'ensembles de cette nature correspond au i-ème coefficient binomial de rang n. Pour chaque élément de l'ensemble il existe d - 1 lettres possibles. On en déduit, si V_t désigne le cardinal d'une boule fermée de rayon t :

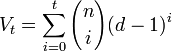
Pour que le code puisse corriger t erreurs, ces boules doivent être disjointes. Le cardinal de leur réunion est égal à M.V_t, où M désigne le cardinal du code. Or, cette réunion ne peut pas avoir un cardinal strictement supérieur à celui de l'espace F, ce qui donne lieu à la définition et à la proposition suivante :

• Si M désigne le cardinal du code, alors la majoration suivante est vérifiée, elle porte le nom de borne de Hamming.

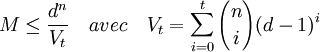
Un code est dit parfait si et seulement si les boules fermées de centres les mots du code et de rayon t forment une partition de F, ce qui donne lieu à la proposition suivante :

• Un code est parfait si et seulement si la borne de Hamming est atteinte.