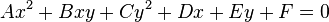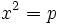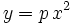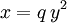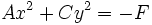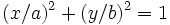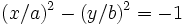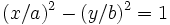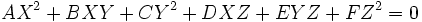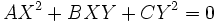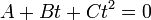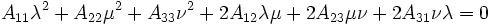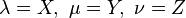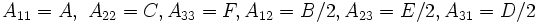Conique - Définition
La liste des auteurs de cet article est disponible ici.
Définition purement projective
Il s'agit de définir les coniques sans distances, sans angles, juste avec la règle, le crayon et une poignée d'axiomes, dans la plus pure tradition de Blaise Pascal et Girard Desargues : voir Traité projectif des coniques.
Définition analytique
Cas affine
En géométrie analytique affine, les coniques sont les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les coordonnées cartésiennes x et y des points sont solution d'une équation polynômiale du second degré, de la forme :
avec l'un au moins des trois coefficients A, B ou C non nul pour que l'équation soit effectivement du second degré ( condition (1) ).
Suivant le repère utilisé, l'expression de l'équation sera plus ou moins simple, mais restera toujours du second degré. Il est intéressant de chercher le repère dans lequel l'expression de l'équation, dite équation réduite, sera la plus simple.
Pour cela, nous pouvons remarquer d'abord qu'il est toujours possible de rendre le coefficient B nul par une rotation du repère.
Nous regardons ensuite les coefficients A et C :
- Si le coefficient C est lui aussi nul, A est alors forcément non nul ( condition (1) ), et une translation suivant l'axe des x permet ainsi d'annuler le coefficient D.
-
- Si E est nul, en posant p = - F / A , l'équation se réduit à :
- Suivant le signe de p, nous obtenons 0 à 2 droites parallèles.
- Si E est non nul, une translation suivant l'axe des y annule F. En posant p = - A / E , nous obtenons l' équation cartésienne réduite d'une parabole :
- Si le coefficient A est nul, on obtient la situation symétrique de la précédente où x et y voient leurs rôles échangés. On obtient donc encore :
-
- Si D est nul, 0 à 2 droites parallèles,
- Si D est non nul, une parabole d'équation réduite :
- Si les coefficients A et C sont tous les deux non nuls, une translation suivant l'axe des x annule D, et une translation suivant les y annule E. L'équation se réduit donc à :
-
- Si A et C sont de même signe :
- - si F est lui aussi du même signe, il n'y a pas de courbe correspondante;
- - si F est nul, la courbe se réduit à un point;
- - si F est de signe opposé, nous pouvons poser a 2 = - F / A et b 2 = - F / C ; nous parvenons ainsi à l' équation cartésienne réduite d'une ellipse :
-
- Si A et C sont de signes opposés :
- - si F est nul, la courbe se réduit à 2 droites sécantes (= qui se croisent);
- - si F est du signe de A, nous pouvons poser a 2 = F / A et b 2 = - F / C ; nous parvenons ainsi à l' équation cartésienne réduite d'une hyperbole :
-
- - si F est du signe de C, nous pouvons poser a 2 = - F / A et b 2 = F / C ; nous parvenons ainsi à l' autre équation cartésienne réduite d'une hyperbole :
-
-
Cas projectif
En géométrie analytique projective, les coniques sont encore les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les points ont des coordonnées projectives X, Y et Z qui vérifient une équation polynômiale homogène du second degré de la forme (voir coordonnées homogènes):
On travaille donc dans le plan projectif où un point générique a pour coordonnées homogènes [X:Y:Z], et deux coordonnées homogènes proportionnelles ([λX:λY:λZ] et [X:Y:Z], pour un certain λ) désignent le même point du plan. Notre plan projectif contient plusieurs exemplaires du plan affine ; notamment l'ensemble des points admettant des coordonnées homogènes de la forme [X:Y:1].
On peut noter alors que pour Z = 1, on retrouve l'équation du cas affine. En fait, on a :
-
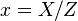
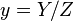
Une première question qu'on se pose est alors : en se limitant à l'image de la conique dans le plan affine ci-dessus défini, quel type de conique affine retrouve-t-on? (et même, retrouve-t-on bien une conique affine?). Pour ce faire, on regarde d'abord leur comportement à l'infini (présence d'asymptotes ou de branches paraboliques,...). Faire tendre x et y vers l'infini revient à faire tendre Z vers 0. Pour Z = 0, l'équation précédente se réduit à :
Cette équation est appelée équations aux directions asymptotiques, car le rapport Y / X donne alors la pente à l'infini de la courbe, c'est-à-dire sa direction asymptotique.
- Si C = 0 :
-
- si B = 0 , l'équation a une solution X = 0 de multiplicité double, ce qui correspond à une pente à l'infini infinie, donc à une direction asymptotique verticale double; la courbe est donc soit une parabole d'axe vertical, soit 0 à 2 droites verticales parallèles;
- si B est non nul, nous obtenons deux directions asymptotiques simples, l'une verticale, l'autre non; la courbe est donc soit une hyperbole, soit 2 droites concourantes;
- Si C est non nul, en posant t = Y / X, l'équation devient :
-
- si le discriminant de cette équation est strictement positif, nous obtenons 2 directions asymptotiques simples distinctes, et la courbe est soit une hyperbole, soit 2 droites concourantes;
- si le discriminant de cette équation est nul, nous obtenons une direction asymptotique double, et la courbe est soit une parabole, soit 0 à 2 droites parallèles;
- si le discriminant de cette équation est strictement négatif, la courbe n'a pas de direction asymptotique, donc pas de branches infinies, et la courbe, si elle existe, est soit une ellipse, soit un point.
-
Cependant, le véritable intérêt de l'utilisation de la géométrie projective est ailleurs. La classification qui a été faite dans le cas affine, et réinterprétée dans le cadre projectif, se base sur des changements de coordonnées affines ; et qui peuvent s'interpréter, le plan affine étant vu comme une partie du plan projectif, comme les changements de coordonnées projectifs qui laissent fixe la droite à l'infini (c'est-à-dire les points du plan projectif de la forme [X,Y,0]). Il existe évidemment beaucoup d'autres changements de coordonnées projectifs, et s'autoriser à les utiliser va permettre d'assouplir grandement la classification des coniques. En fait, la classification des coniques projectives provient directement de celle des forme bilinéaire symétrique sur l'espace vectoriel de dimension 3 sous-jacent à notre plan projectif.
Cas barycentrique
En géométrie analytique barycentrique, les coniques sont toujours les courbes planes algébriques du second ordre, c'est-à-dire les courbes planes dont les points ont des coordonnées barycentriques λ, μ et ν qui vérifient une équation polynômiale homogène du second degré de la forme :
On peut identifier cette équation à la précédente, en posant :
On obtient alors, à un coefficient multiplicatif près :