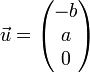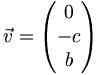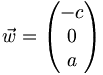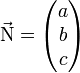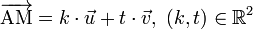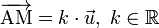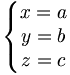Géométrie analytique - Définition

Introduction

La géométrie analytique est une approche de la géométrie dans laquelle les objets sont représentés par des équations ou des inéquations. Elle est fondamentale pour la physique et l'infographie.

En géométrie analytique le choix d'un repère est indispensable. Tous les objets seront décrits relativement à ce repère, à l'aide de coordonnées.

Histoire

L'analyse en géométrie

Le terme de géométrie analytique, par opposition à la géométrie synthétique, se refère aux méthodes d'analyse et synthèse pratiquées par les géomètres grecs. Elle en est progressivement venue à se confondre avec sa méthode privilégiée, la méthode des coordonnées.

Dans les mathématiques grecques, l'analyse consiste à partir de l'objet cherché, en supposant son existence, de manière à établir ses propriétés. Il faut poursuivre dans cette voie jusqu'à produire assez de propriétés pour caractériser l'objet. On peut alors renverser la situation, en ne faisant plus l'hypothèse d'existence et en l'introduisant effectivement l'objet par le biais des propriétés caractéristiques : c'est la phase de synthèse, qui doit aboutir à la preuve d'existence.

La difficulté pratique qui a limité les progrès des géomètres est le manque d'un formalisme adapté à la description des relations entre grandeurs géométriques. François Viète, à la fin du XVI^e siècle unifie le calcul sur les nombres et le calcul sur les grandeurs géométriques à travers un outil précieux, le calcul littéral. Le principe de la réduction au calcul algébrique est posé, il manque encore une méthode systématique pour l'exploiter.

La méthode des coordonnées

Marino Ghetadi, puis René Descartes proposent de résoudre les problèmes de géométrie par le recours systématique au calcul algébrique. Dans sa Géométrie de 1637, le philosophe en formule le principe. Il s'agit de représenter grandeurs connues et inconnues par des lettres, et de trouver autant de relations entre grandeurs connues et inconnues qu'il y a d'inconnues au problème. On y reconnaît bien une démarche analytique, conduisant à des systèmes d'équations qu'il s'agit de réduire à une seule équation. Descartes donne des interprétations des cas sur- ou sous-déterminés. Ses manipulations, cependant, se limitent aux équations algébriques, qu'il classe par degré, et ne peuvent être appliquées aux courbes qu'il qualifie de mécaniques (aujourd'hui dites transcendantes).

Pierre de Fermat est le premier à faire, à la même époque, un usage systématique des coordonnées proprement dites pour résoudre les problèmes de lieux géométriques. Il fait intervenir notamment les premières équations de droites, paraboles ou hyperboles. Il présente ces idées dans Ad locus planos et solidos isagoge, en 1636, texte publié après sa mort.

Dans les notations de Descartes, contrairement à Fermat, les constantes sont continuellement notées a, b, c, d, ... et les variables x, y, z. Il s'oppose en cela à la tradition de l'époque et un lecteur d'aujourd'hui s'en trouve moins dérouté.

Géométrie analytique dans l'espace

L'espace affine est muni d'un repère  ; x désigne l'abscisse d'un point, y l'ordonnée et z la cote.

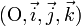
Plan

Un plan affine (c'est-à-dire un plan au sens habituel en géométrie, composé de points) est représenté par une équation du premier degré à trois inconnues :

ax + by + cz + d = 0 (3)

Si deux plans sont parallèles entre eux, alors ils ont des vecteurs normaux multiples, alors leurs coefficients a, b et c sont proportionnels. Si d est nul, alors le plan passe par l'origine O. Si c est non nul, l'équation peut s'écrire :

z = a′·x + b′·y + c′

avec a′ = - a/c, b′ = - b/c et c′ = - d/c. Si c est nul, alors on a un plan vertical.

Un plan vectoriel (c'est-à-dire un ensemble de vecteurs coplanaires) est représenté par une équation

au₁ + bu₂ + cu₃ = 0

où u₁, u₂ et u₃ sont les composantes d'un vecteur. Les vecteurs suivants sont des vecteurs du plan vectoriel, et si au moins deux coefficients de l'équation du plan sont non nuls, deux de ces vecteurs forment une base du plan :

(la base obtenue n'est a priori pas orthonormée). Ces vecteurs forment aussi des vecteurs d'un plan affine dont l'équation a les mêmes coefficients a, b et c que l'équation du plan vectoriel.

Si deux des coefficients sont nuls, alors l'équation se réduit à l'une des trois formes suivantes :

u₁ = 0, qui représente le plan vectoriel  ;

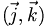
u₂ = 0, qui représente le plan vectoriel  ;

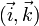
u₃ = 0, qui représente le plan vectoriel .

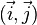
De même,

ax + d = 0 représente un plan affine parallèle à , dont l'équation peut s'écrire x = - d/a

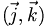
by + d = 0 représente un plan affine parallèle à , dont l'équation peut s'écrire y = - d/b

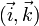
cz + d = 0 représente un plan affine parallèle à , dont l'équation peut s'écrire z = - d/c.

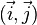
Dans tous les cas, si le repère de l'espace est orthonormal, le vecteur

est un vecteur normal au plan

Quel que soit le repère, si le plan passe par un point A(x_A, y_A, z_A) et est muni d'une base quelconque , alors pour tout point M(x_M, y_M, z_M), on a

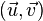
puisque , et sont coplanaires. Ceci conduit à l'équation paramétrique

(4)

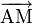
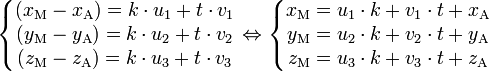
Droite

Une droite étant l'intersection de deux plans non-parallèles, elle est décrite par un système de deux équations du premier degré à trois inconnues :

(5)

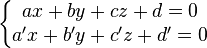
La droite est contenue dans les deux plans, elle est donc orthogonale aux vecteurs normaux et des deux plans. Le produit vectoriel des vecteurs normaux fournit donc un vecteur directeur de la droite. Si le repère est orthonormé direct, le vecteur a pour composantes :

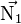
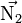
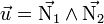
Si par ailleurs on connaît un point A(x_A, y_A, z_A) et un vecteur directeur de la droite, alors si M(x_M, y_M, z_M) est un point de la droite, il vérifie :

puisque et sont colinéaires. On obtient donc l'équation paramétrique :

(6)

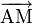
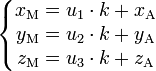
Point

Un point étant l'intersection de trois plans, il est décrit par un système de trois équations du premier degré à trois inconnues :

Le point étant l'intersection de trois plans concourants, ses coordonnées doivent vérifier les trois équations ; la réduction de ce système donne la forme ci-dessus. Ce système d'équations représente bien sûr le point (a,b,c).