Coordonnées cartésiennes - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Abscisse sur une droite affine - Coordonnées cartésiennes dans l'espace - Coordonnées cartésiennes dans le plan - Cinématique - Coordonnées cartésiennes en dimension n

Introduction

En coordonnées cartésiennes planaires, la position d'un point A est donnée par les distances xA et yA.

En coordonnées cartésiennes tridimensionnelles, la position d'un point P est donnée par les distances x, y et z.

Un système de coordonnées cartésiennes permet de déterminer la position d'un point sur une droite, dans un plan ou dans l'espace à condition d'avoir défini un repère cartésien. Il permet aussi de caractériser un vecteur. La notion de coordonnées cartésiennes peut aussi se généraliser à un espace de dimension n. Le mot cartésien vient du mathématicien et philosophe français René Descartes. Il existe d'autres systèmes de coordonnées permettant de repérer un point dans le plan ou dans l'espace

Abscisse sur une droite affine

Sur une droite affine D, un repère est la donnée de :

Une origine O, id est un point distingué de D.
Un vecteur v de la droite vectorielle directrice $\vec D$ . Ce vecteur porte deux informations :
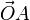
- Une orientation : un point A est à droite de O lorsque le vecteur $\vec OA$ est positivement colinéaire à v.
- Une unité : un point A est à la distance r de O lorsque $\vec{OA}=\pm r\cdot v$

Dans ce cas, l'abscisse du point M est l'unique réel r tel que : $\vec{OM}=r\cdot v$ . Il y a donc une correspondance entre les points d'une droite affine et l'ensemble des réels.

Remarque : Il existe des systèmes de graduation non régulière mais le repère n'est plus appelé cartésien (voir échelle logarithmique).

Coordonnées cartésiennes dans l'espace

Le principe de construction sera le même. Dans un espace affine E de dimension 3, un repère (cartésien) est la donnée conjointe de :

un point d'origine O,
et trois vecteurs non coplanaires i, j, et k.

Les axes de coordonnées sont les droites affines concourantes (Ox)=(O,i), (Oy)=(O,j) et (Oz)=(O,k).

Pour un point M, on est en droit de tracer :

un plan parallèle au plan (Oyz) qui coupe (Ox) en m_x d'abscisse x,
un plan parallèle au plan (Oxz) qui coupe (Oy) en m_y d'abscisse y,
un plan parallèle au plan (Oxy) qui coupe (Oz) en m_z d'abscisse z.

Le triplet de réels (x,y,z) est uniquement déterminé par la position du point M. Il s'appelle les coordonnées (cartésiennes) de M dans le repère (O,i,j,k) :

le réel x s'appelle l'abscisse.
le réel y s'appelle l'ordonnée ou la profondeur.
le réel z s'appelle la cote ou la hauteur.

Réciproquement, à tout triplet de réels (x,y,z) correspond un unique point M d'abscisse x, d'ordonnée y et de cote z. Ce point s'obtient comme l'intersection :

du plan parallèle au plan (Oyz) passant par le point de (Ox) d'abscisse x,
du plan parallèle au plan (Oxz) passant par le point de (Oy) d'abscisse y et
du plan parallèle au plan (Oxy) passant par le point de (Oz) d'abscisse z.

Ces trois plans ainsi que les trois plans de bases (Oxy), (Oxz) et (Oyz) dessinent un parallélépipède.

Il y a correspondance biunivoque entre tout point M et tout triplet de réels appelés alors système de coordonnées de M.

De même que dans le plan, ces coordonnées se réinterprètent via l'écriture vectorielle :

Repères orthonormés

Dans un espace affine euclidien de dimension 3, un repère (O,i,j, k)) est dit orthonormé lorsque les vecteurs i, j, et k sont unitaires et deux à deux orthogonaux. Cette deuxième condition s'écrit :

;

Comme dans le plan, il sera nécessaire de prendre un repère orthonormé si l'on désire travailler sur des distances et des angles. La distance s'écrira alors: