Constantes d'Oort - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les constantes d'Oort ou paramètres d'Oort sont des coefficients qui mesurent les propriétés du champ de vitesse dans le disque galactique au voisinage solaire. Ils sont nommés en l'honneur de l'astronome hollandais Jan Oort qui les a introduits en 1927 en démontrant par là même la réalité de la rotation des étoiles autour du centre de la Voie lactée.
Dans l'hypothèse où les trajectoires des étoiles dans les galaxies sont circulaires et que leur vitesse ne dépend que de leur distance au centre, il est possible observationnellement de déterminer la vitesse angulaire des étoiles dans le voisinage solaire ainsi que sa dépendance locale par rapport à la distance du Soleil au centre galactique par la seule observation de la vitesse radiale et du mouvement propre d'autres étoiles proches par rapport au Soleil.
Formule
Les constantes d'Oort sont au nombre de deux, notées A et B suivant les notations introduites par Oort en 1927. Elles interviennent dans la valeur prédite de la vitesse radiale V (mesurable par spectroscopie) et la vitesse tangentielle
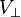
- Vr = rAsin(2(l − l0)),
-
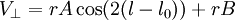
où l représente une longitude galactique dans un système de coordonnées galactiques dans lequel le centre galactique (a priori indéterminé) est situé à la longitude l.
Les constantes d'Oort A et B ont la dimension d'une vitesse divisée par une longueur et s'expriment traditionnellement en km⋅s-1⋅kpc-1. Elles sont reliés à la vitesse orbitale V au voisinage solaire et sa dérivée par rapport à la distance R au centre par :
-
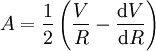
-
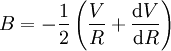
ces valeurs étant évaluées au voisinage solaire.
On se place dans la plan galactique dans lequel le centre galactique est à la longitude l. Les coordonnées du Soleil dans ce plan sont donc :
-
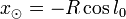
-
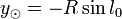
On suppose le Soleil animé d'un mouvement circulaire de vitesse V, et on définit l'orientation des coordonnées galactiques par le fait que le Soleil se dirige vers la direction l = 90°dont les coordonnées sont donc
-
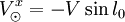
-
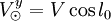
Soit une étoile, dont le mouvement est également supposé circulaire, situé à une distance r du Soleil et à la longitude l. On suppose la distance de l'étoile r petite devant la distance au centre galactique R. Les coordonnées de l'étoile dans le plan galactique sont
- x * = − Rcosl0 + rcosl,
- y * = − Rsinl0 + rsinl.
La distance de cette étoile au centre galactique est approximativement
- D * = R − rcos(l − l0).
La vitesse de cette étoile par rapport au centre galactique est, en valeur absolue,
-
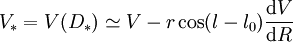
L'angle fait la direction étoile-centre galactique diffère de la direction Soleil-centre galactique par la valeur
-
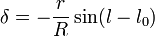
de sorte que les coordonnées de la vitesse de l'étoile s'écrivent
-
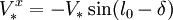
-
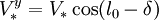
La vitesse relative de l'étoile par rapport au soleil est donc
- δVx = − V * sin(l0 − δ) + Vsinl0,
- δVy = V * cos(l0 − δ) − Vcosl0.
En développant ces expressions et en ne gardant que les termes de l'ordre le plus bas, il vient
-
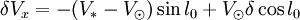
-
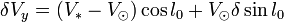
La composante de cette vitesse relativement à la direction de l'étoile donne la vitesse radiale de celle-ci. Elle vaut
- Vr = δVxcosl + δVysinl.
Elle vaut
-
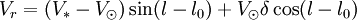
En remplaçant les termes
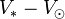
-
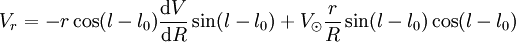
que l'on peut combiner en
-
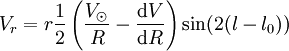
ou bien
- Vr = rAsin(2(l − l0)),
en utilisant la définition de A ci-dessus.
La composante perpendiculaire de vitesse se calcule selon
-
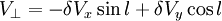
ce qui donne
-
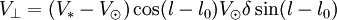
En remplaçant à nouveau les deux quantités par leurs valeurs précédemment trouvées, il vient
-
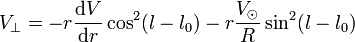
qui se combine en
-
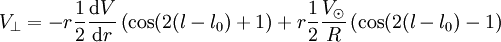
soit
-