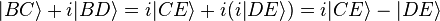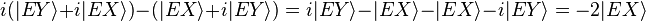Contrafactualité (physique) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Mécanique quantique | ||||||||||||||
| | ||||||||||||||
| Postulats de la mécanique quantique Histoire de la mécanique quantique
| ||||||||||||||
Selon la mécanique quantique, des évènements contrefactuels, qui auraient pu se produire mais qui ne se sont pas produits, influent sur les résultats de l'expérience. Ce phénomène a été choisi par le magazine New Scientist comme une des "sept merveilles du monde quantique".
Problème d'Elitzur-Vaidman
Exposé du problème
Considérons le dispositif suivant :
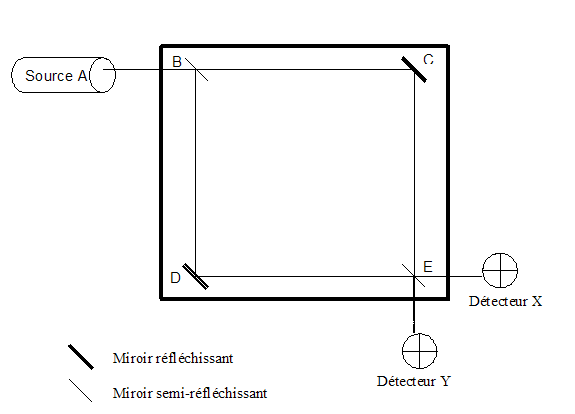
Un photon unique est émis par la Source A. On peut démontrer (et vérifier expérimentalement) que seul le détecteur X enregistre la sortie du photon de ce dispositif. Si on ne considère pas les lois quantiques, les détecteurs X et Y auraient une chance égale de détecter le photon à la sortie du dispositif. Ce phénomène est dû à l’état superposé que prend le photon à la sortie du miroir semi réfléchissant B : |\Photon transmis> + |Photon réfléchi>. Une interférence, du même type que celle de l’expérience des fentes d'Young, a alors lieu en E et rend nulle la probabilité que le photon soit détecté en Y.
Une réflexion sur un miroir introduit un déphasage de 1/4 de longueur d'onde. Soit la notation
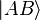
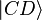
On a alors
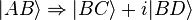
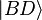
Or
-
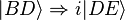
-
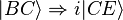
donc
Cette fonction d'onde représente l'état superposé du quanta juste avant d'arriver sur E.
D'autre part, on a :
-
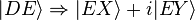
-
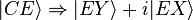
donc l'état superposé juste avant E
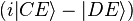
Au final :
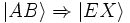
Cette expérience est très semblable dans l’esprit à celle des fentes d'Young, mais permet de plus de mettre en évidence la contrafactualité des phénomènes quantiques :
Modifions ce dispositif pour que C soit maintenant un détecteur de photon, du même type que X ou Y. On constate alors (théoriquement et expérimentalement) les faits suivants :
- Soit le photon est détecté par C (probabilité ½)
- Soit les détecteurs X et Y ont une chance égale de détecter le photon (probabilité ¼ et ¼)
C’est ici qu’intervient la contrafactualité : si un photon est détecté en Y, c’est donc que le détecteur C aurait pu détecter le photon (mais il ne l’a pas détecté, sinon le photon n’aurait pu être détecté par Y, ayant déjà été détecté en C). Un évènement contrafactuel modifie donc bel et bien les résultats de l’expérience.
Une variante de ce dispositif est le problème d’Elitzur-Vaidman. Admettons que l’on fabrique des bombes atomiques qui soient déclenchées par un détecteur ultrasensible : la bombe explose si un seul photon est détecté par le détonateur. Ce détecteur possède également les propriétés suivantes :
- Il est peu fiable (mais soit il fonctionne toujours, soit il ne fonctionne jamais)
- S’il ne fonctionne pas, il se comporte comme le miroir réfléchissant C
- Il n’y a pas d’autre moyen de tester ce détecteur qu’en l’utilisant associé à la bombe.
Le gouvernement veut disposer d’un stock de bombes fiables, dont le fonctionnement du détecteur est garanti. Comment tester le détecteur sans faire exploser toutes les bombes fiables ?
La physique quantique nous en donne le moyen : plaçons une bombe en C, et envoyons un photon en A. Si le photon est détecté en Y c’est que le détecteur de la bombe aurait pu détecter le photon, et donc la bombe est certifiée 100% fiable. Mais elle n’a pas explosé.
Si le photon est détecté par X, on ne peut conclure sur la fiabilité de la bombe. Bien entendu, si la bombe explose c’est qu’elle était fiable. En itérant le processus, en remettant en jeu les bombes n’ayant pas explosé et associées à une détection en X, on peut certifier jusqu’à 1/4 + 1/4.1/4 + 1/4.1/4.1/4 + … = 1/3 des bombes initiales.