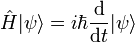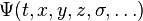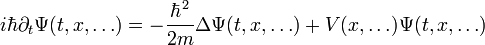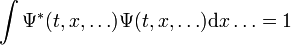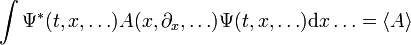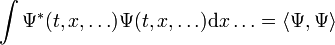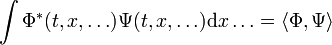Notation bra-ket - Définition

Introduction

Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Cette boîte : voir • disc. • mod.

La notation bra-ket a été introduite par Paul Dirac pour faciliter l’écriture des équations de la mécanique quantique, mais aussi pour souligner l’aspect vectoriel de l’objet représentant un état quantique (voir Axiomes de la mécanique quantique).

Le nom provient d'un jeu de mots avec le terme (en) bracket qui signifie « crochet de parenthèse », en l'occurrence «   » et «   » respectivement appelés « bra » et « ket » (un peu à l'image de bâbord et de tribord). Cette notation est depuis reprise dans l’étude mathématique de l’algèbre des opérateurs, dont le champ d’application est plus large.

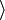
L'origine du formalisme

Notation : la notation * signifie qu'il est question du transposé du conjugué d'un vecteur dont les coordonnées sont des nombres complexes.

On rappelle que les fonctions d'onde quantiques sont des fonctions du temps, des coordonnées spatiales, voire d'autres paramètres internes (spins, moments magnétiques, …) :

qu'elles sont solutions de l'équation de Schrödinger :

qu'elles sont normalisées, de sorte que :

et que la valeur d'une grandeur physique A est obtenue par :

La notation de Dirac s'appuie sur l'identification de l'intégrale précédente avec un produit hermitien sur l'espace des fonctions à valeur complexe de carré intégrable L² :

et par généralisation à deux fonctions Φ(t,...) et Ψ(t,...) :

noté en mécanique quantique : On identifie donc :

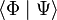
• la fonction Ψ(t,x,y,z,σ,...) avec un vecteur formel dénommé ket Ψ.
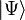
• la fonctionnelle duale avec dénommé bra Φ, dual du ket Ψ.

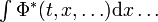
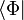
D'autre part sous le formalisme de Heisenberg, les solutions ne sont plus des fonctions, mais les vecteurs d'un espace de vecteurs d'états, ce qui rend l'identification encore plus directe.