Courbe de Hilbert - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

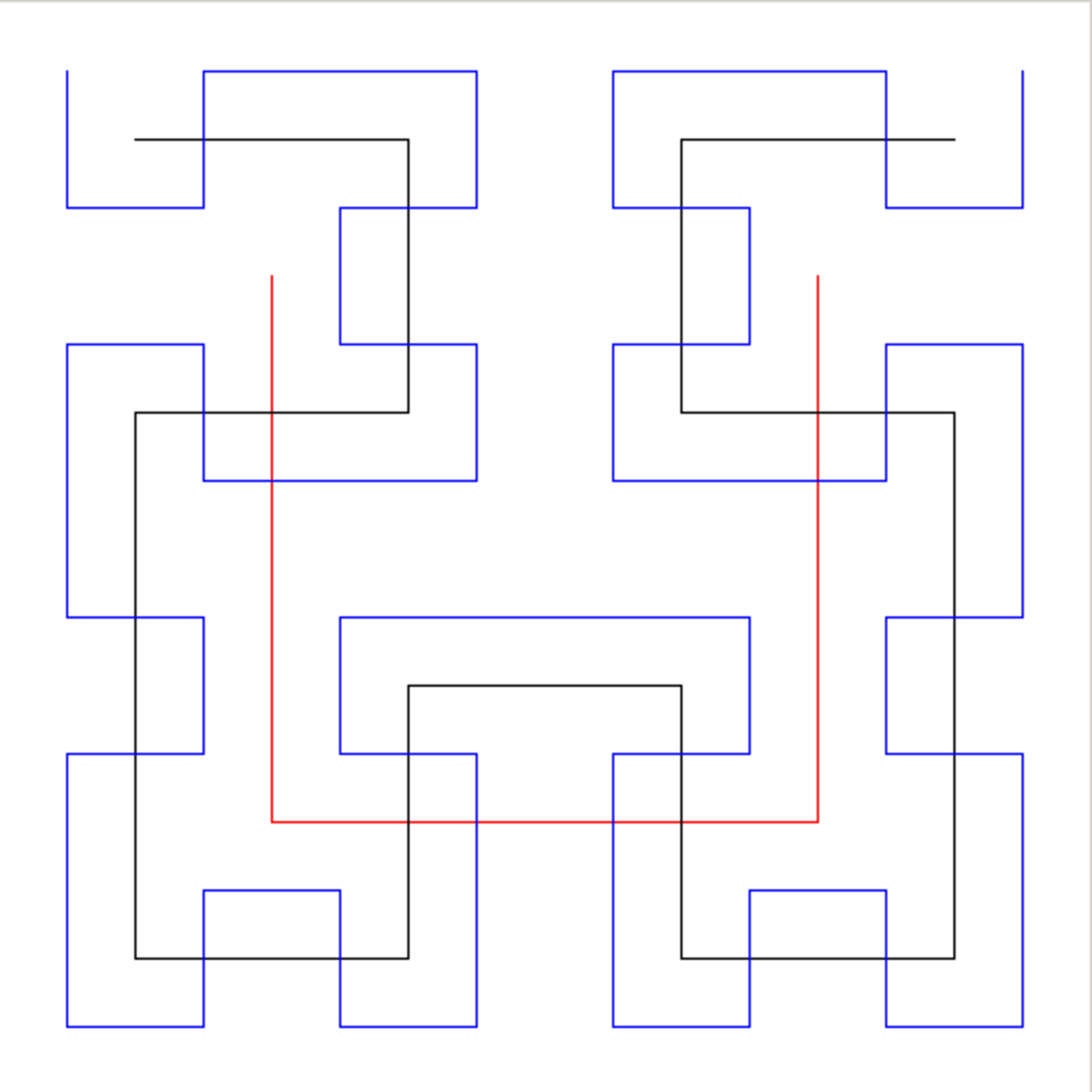

La Courbe de Hilbert est une courbe fractale continue remplissant le plan. Elle a été décrite pour la première fois par le mathématicien allemand David Hilbert en 1891.
Comme elle couvre un plan, sa dimension de Hausdorff (à la limite
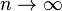
La longueur euclidienne de Hn est
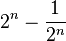
Pour les bases de données multi-dimensionnelles, la courbe de Hilbert a été proposée à la place de la courbe de Lebesgue parce qu'elle a un comportement préservant mieux la localité.
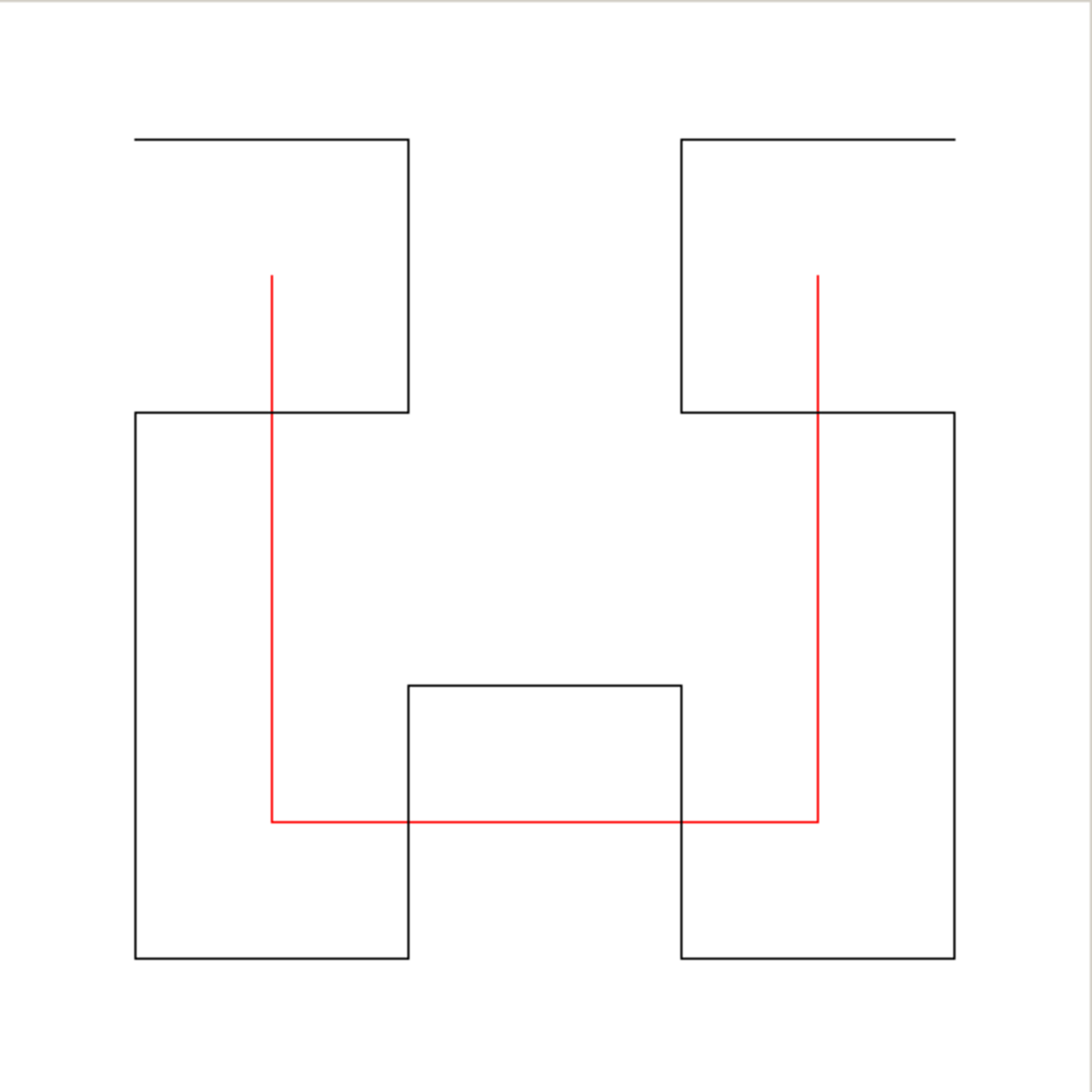
Representation en L-Système
La courbe de Hilbert peut être construite par un L-système
- Alphabet : L, R
- Constantes : F, +, −
- Axiome : L
- Règles:
- L → +RF−LFL−FR+
- R → −LF+RFR+FL−
Ici, F signifie "avance", + signifie "à gauche 90°", et - signifie "à droite 90°"
Programme
Butz propose un algorithme pour calculer la courbe de Hilbert en plusieurs dimensions.
Le programme Java suivant trace une courbe de Hilbert par quatre méthodes qui s'appellent récursivement :
import java.awt.*; import java.applet.*; public class HilbertCurve extends Applet { private SimpleGraphics sg=null; private int dist0=512, dist=dist0; public void init() { dist0 = 512; resize ( dist0, dist0 ); sg = new SimpleGraphics(getGraphics()); } public void paint(Graphics g) { int level=4; dist=dist0; for (int i=level;i>0;i--) dist /= 2; sg.goToXY ( dist/2, dist/2 ); HilbertU(level); // start recursion } // Trace courbe "U" à cette échelle: private void HilbertU(int level) { if (level > 0) { HilbertD(level-1); sg.lineRel(0,dist); HilbertU(level-1); sg.lineRel(dist,0); HilbertU(level-1); sg.lineRel(0,-dist); HilbertC(level-1); } } // Trace courbe "]" à cette échelle: private void HilbertD(int level) { if (level > 0) { HilbertU(level-1); sg.lineRel(dist,0); HilbertD(level-1); sg.lineRel(0,dist); HilbertD(level-1); sg.lineRel(-dist,0); HilbertA(level-1); } } // Trace courbe "[" à cette échelle: private void HilbertC (int level) { if (level > 0) { HilbertA(level-1); sg.lineRel(-dist,0); HilbertC(level-1); sg.lineRel(0,-dist); HilbertC(level-1); sg.lineRel(dist,0); HilbertU(level-1); } } // Trace courbe "⊓" à cette échelle: private void HilbertA (int level) { if (level > 0) { HilbertC(level-1); sg.lineRel(0,-dist); HilbertA(level-1); sg.lineRel(-dist,0); HilbertA(level-1); sg.lineRel(0,dist); HilbertD(level-1); } } } class SimpleGraphics { private Graphics g = null; private int x = 0, y = 0; public SimpleGraphics(Graphics g) { this.g = g; } public void goToXY(int x, int y) { this.x = x; this.y = y; } public void lineRel(int deltaX, int deltaY) { g.drawLine ( x, y, x+deltaX, y+deltaY ); x += deltaX; y += deltaY; } }
Et voici une autre version qui met en œuvre les règles du L-système :
def f walk 10 end def p turn 90 end def m turn -90 end def l(n) return if n==0 p; r(n-1); f; m; l(n-1); f; l(n-1); m; f; r(n-1); p end def r(n) return if n==0 m; l(n-1); f; p; r(n-1); f; r(n-1); p; f; l(n-1); m end l(6)