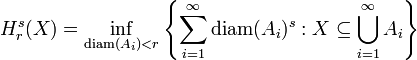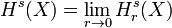Dimension de Hausdorff - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La dimension de Hausdorff d'un espace métrique (X,d) est, en topologie, un nombre réel positif ou nul, éventuellement l'infini. Introduite en 1918 par le mathématicien Felix Hausdorff, elle a été développée par Abram Samoilovitch Besicovitch. Elle est parfois appelée dimension de Hausdorff-Besicovitch.
Un espace vectoriel réel de dimension finie E peut être muni d'une norme et toutes les normes sur E sont équivalentes. La dimension de Hausdorff de E fait sens et vaut la dimension de E - telle qu'elle est définie en algèbre linéaire. Cependant, en général, la dimension de Hausdorff n'est pas entière. Par exemple, la dimension de Hausdorff d'une courbe peut être strictement supérieure à 1. Il est possible de rencontrer des espaces métriques compacts de dimension 0 qui ne soient pas finis.
Introduction informelle
Dans un espace euclidien de dimension d, une boule de rayon r a un volume proportionnel à rd. Intuitivement, on s'attend donc à ce que le nombre N(r) de boules de rayon r nécessaires pour recouvrir une boule de rayon unité soit de l'ordre de 1 / rd.
On généralise cette notion à un espace métrique compact X quelconque de la façon suivante. Posons N(r) le nombre minimal de boules ouvertes de rayon r nécessaires pour recouvrir X. Si, lorsque r tend vers 0, N(r) croît comme
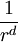
Propriétés
- Si X est inclus dans
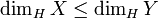
- La dimension de Hausdorff d’un produit d’espaces métriques est supérieure ou égale à la somme des dimensions de Hausdorff.
- Explicitement, pour tous espaces métriques
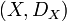
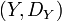
-
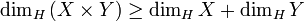
- Explicitement, pour tous espaces métriques
- Si X est inclus dans
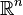
- Si X est une réunion dénombrable de parties, toutes de dimension inférieure ou égale à n, alors
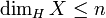
- Une fonction lipschitzienne diminue la dimension de Hausdorff.
- Plus généralement, si
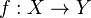

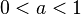
-
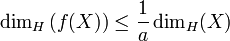
- Plus généralement, si
Soit s strictement positif tel que  , il existe un recouvrement ouvert dénombrable
, il existe un recouvrement ouvert dénombrable
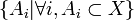
 tel que :
tel que :
-
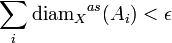
Comme



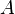
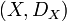
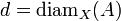
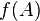
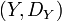
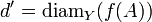
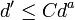
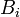
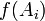
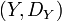
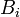
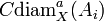
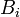
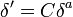
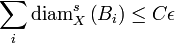
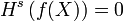
 .
.- La dimension de Hausdorff n'est pas une quantité conservée par homéomorphisme. Par exemple, on peut définir des ensembles de Cantor, homéomorphes entre eux, mais de dimensions différentes. Mais si l'homéomorphisme ainsi que sa réciproque sont tous deux lipschitiziens, alors la distance est conservée.
- Si deux métriques sont Lipschitz-équivalentes, alors elles définissent la même dimension de Hausdorff.
Définition
Malheureusement, les limites des quantités N(r)rs introduites dans le paragraphe précédent n'existent pas toujours. On peut contourner cette difficulté en procédant de la façon suivante :
- On recouvre l'espace X au moyen d'une réunion dénombrable de parties notées Ai, chacune étant de diamètre inférieur à r. Le fait d'utiliser une majoration du diamètre permet de prendre des parties arbitrairement petites, par exemple s'il s'agit de recouvrir une partie dénombrable de X, et de minimiser ainsi le rôle d'une telle partie dans le calcul de la dimension de X. Pour tout s réel positif ou nul, on considère la quantité
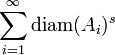
- La fonction Hs est décroissante, ce qui assure l'existence d'une limite (éventuellement infinie) quand on fait tendre r vers 0. D'où la définition :
-
-
- Hs s'appelle mesure de Hausdorff. On vérifie que, si Hs(X) est fini, alors pour tout t > s, Ht(X) = 0, et que, si Hs(X) > 0, alors pour tout t < s, Ht(X) est infini.
- Il existe donc un nombre séparant les nombres s pour lesquels Hs(X) = 0 de ceux pour lesquels Hs(X) est infini. Ce nombre est la dimension de Hausdorff de X. On pose donc :
-
-
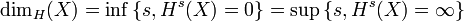
-