Fractale - Définition

Introduction

Un exemple de fractales.

On nomme figure fractale ou "fractale" par substantivation de l'adjectif (ou encore en anglais fractal), une courbe ou surface de forme irrégulière ou morcelée qui se crée en suivant des règles déterministes ou stochastiques impliquant une homothétie interne. Le terme « fractale » est un néologisme créé par Benoît Mandelbrot en 1974 à partir de la racine latine fractus, qui signifie brisé, irrégulier (fractales n.f). Dans la « théorie de la rugosité » développée par Mandelbrot, une fractale désigne des objets dont la structure est liée à l'échelle.

Ce terme était au départ un adjectif : les objets fractals (selon un pluriel formé sur l'exemple de "chantiers navals"). Les fractales sont définies de manière paradoxale, en référence aux structures gigognes dont ils constituent des cas particuliers : « Les objets fractals peuvent être envisagés comme des structures gigognes en tout point –et pas seulement en un certain nombre de points, les attracteurs de la structure gigogne classique. Cette conception hologigogne (gigogne en tout point) des fractales implique cette définition tautologique : un objet fractal est un objet dont chaque élément est aussi un objet fractal ». Malgré les apparences, ce type de définitions de nature récursive n'est pas seulement théorique mais peut concerner aussi des concepts usuels : un ancêtre est un parent ou un ancêtre d'un parent, un multiple est un composé d'un nombre ou d'un multiple de ce nombre, un escalier commence ou prolonge un escalier, une dynastie inaugure ou prolonge une dynastie, etc.

Caractéristiques

Construction animée : courbe de von Koch

Un objet fractal possède au moins l'une des caractéristiques suivantes :

• sa dimension de Hausdorff est strictement supérieure à sa dimension topologique. Cette caractéristique est généralement prise comme définition même d'un objet fractal. Pour exprimer la chose autrement, un réseau d'irrigation est un déploiement de lignes (« en 1D ») qui offre des caractéristiques commençant à évoquer une surface (« en 2D »). La surface du poumon (« en 2D ») est repliée en une sorte de volume (« en 3D »). De façon imagée, les fractales se caractérisent par une sorte de dimension non-entière.
• il a des détails similaires à des échelles arbitrairement petites ou grandes ;
• il est trop irrégulier pour être décrit efficacement en termes géométriques traditionnels ;
• il est exactement ou statistiquement autosimilaire, c'est-à-dire que le tout est semblable à une de ses parties ;

Dimension fractale

Ensemble de Julia

La dimension d'une ligne droite, d'un cercle et d'une courbe régulière est de 1. Une fois fixé une origine et un sens, chaque point de la courbe peut être déterminé par un nombre, qui définit la distance entre l'origine et le point. Le nombre est pris négativement s'il faut se déplacer dans le sens opposé à celui choisi au départ.

La dimension d'une figure simple dans le plan est de 2. Une fois un repère défini, chaque point de la figure peut être déterminé par deux nombres. La dimension d'un corps simple dans l'espace est de 3.

Une figure telle qu'une fractale n'est pas simple. Sa dimension n'est plus aussi facile à définir et n'est plus forcément entière. La dimension fractale, plus complexe, s'exprime à l'aide de la dimension de Hausdorff.

Quand la fractale est formée de répliques d'elle-même en plus petit, sa dimension fractale peut se calculer comme suit :

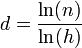
où la fractale de départ est formée de n exemplaires dont la taille a été réduite d'un facteur h (pour homothétie).

Quelques exemples :

• Un côté du flocon de Koch est formé de n = 4 exemplaires de lui-même réduit d'un facteur h = 3. Sa dimension fractale vaut :

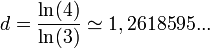
• Le triangle de Sierpinski est formé de n = 3 exemplaires de lui-même réduit d'un facteur h = 2 . Sa dimension fractale vaut :

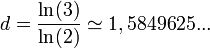
• Le tapis de Sierpinski est formé de n = 8 exemplaires de lui-même réduit d'un facteur h = 3. Sa dimension fractale vaut :

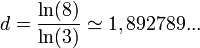
Une liste beaucoup plus longue se trouve sous : Liste de fractales par dimension de Hausdorff.