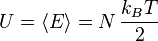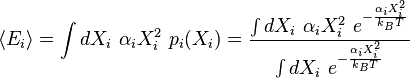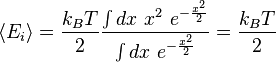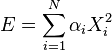Vendredi 2 Mai 2025
Rechercher 🔍

Degré de liberté (physique et chimie) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - En mécanique - Degrés de liberté indépendants - En mécanique et thermodynamique statistiques - Théorème d'équipartition - Degrés de liberté quadratiques

Théorème d'équipartition

En physique statistique classique, à l'équilibre thermodynamique, l'énergie interne d'un système de N degrés de liberté indépendants et quadratiques est :

U = \langle E \rangle = N\,\frac{k_B T}{2}

Démonstration

Ici, l'énergie moyenne associée avec un degré de liberté est :

\langle E_i \rangle = \int dX_i\,\,\alpha_i X_i^2\,\, p_i(X_i) = \frac{\int dX_i\,\,\alpha_i X_i^2\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}{\int dX_i\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}
\langle E_i \rangle = \frac{k_B T}{2}\frac{\int dx\,\,x^2\,\, e^{-\frac{x^2}{2}}}{\int dx\,\, e^{-\frac{x^2}{2}}} = \frac{k_B T}{2}

Les degrés de libertés étant indépendants, l'énergie interne du système est égale à la somme de l'énergie moyenne associée à chaque degré de liberté, ce qui démontre le résultat.

Degrés de liberté quadratiques

Un degré de liberté Xi est quadratique si les termes d'énergie associés peuvent être écrits :

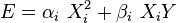
E = \alpha_i\,\,X_i^2 + \beta_i \,\, X_i Y ,

où Y est une combinaison linéaire d'autres degrés de liberté quadratiques.
Par exemple, si X1 et X2 sont deux degrés de liberté, et E l'énergie associé :

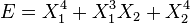
  • Si E = X_1^4 + X_1^3 X_2 + X_2^4 , alors les deux degrés de liberté ne sont pas indépendants et ne sont pas quadratiques.
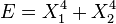
  • Si E = X_1^4 + X_2^4 , les degrés de liberté sont indépendants et non quadratiques.
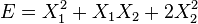
  • Si E = X_1^2 + X_1 X_2 + 2X_2^2 , les degrés de liberté ne sont pas indépendants et sont quadratiques.
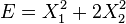
  • Si E = X_1^2 + 2X_2^2 , les degrés de liberté sont indépendants et quadratiques.

En mécanique

En mécanique classique, les dynamique d'un système de degrés de liberté quadratiques sont contôlées par un ensemble d'équations différentielles linéaires avec des coefficients constants.

Degrés de libertés quadratiques et indépendants

X_1, \ldots, X_N sont des degrés de liberté quadratiques et indépendants si l'énergie associée à un micro-état du système qu'ils décrivent peut être écrite :

E = \sum_{i=1}^N \alpha_i X_i^2
En mécanique et thermodynamique statistiques
- Introduction - En mécanique - Degrés de liberté indépendants - En mécanique et thermodynamique statistiques - Théorème d'équipartition - Degrés de liberté quadratiques
miniature
La face cachée de la Lune révèle une étrangeté 🌓
miniature
Piéger le CO2 sous terre indéfiniment, c'est possible ! 🌍
miniature
La plus lointaine cousine de la Voie Lactée jamais observée 🌀
miniature
Ce codex médiéval cache un secret dans son bois 🔍
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
Page générée en 0.091 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise