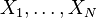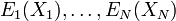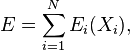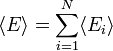Degré de liberté (physique et chimie) - Définition

Introduction

L'expression degré de liberté recouvre la notion indiquant la possibilité pour un système d'évoluer dans une direction non contrainte (en fonction donc d'un paramètre), et implique par conséquent la possibilité de dénombrer ces paramètres. Cette notion est utilisée en chimie, mathématiques et physique.

En mécanique

La notion de degré de liberté est couramment employée, et tout particulièrement en mécanique. Elle recouvre deux considérations :

• pour chaque particule appartenant à un système, et pour chaque direction indépendante dans laquelle un mouvement est possible, deux degrés de liberté sont définis, l'un décrivant la quantité de mouvement dans la direction, l'autre décrivant la position de la particule le long d'un axe défini dans cette direction.
• en ingénierie mécanique, les degrés de liberté indiquent les différentes possibilités de mouvement dans l'espace. Se référer à l'article degré de liberté (mécanique). Cette utilisation de l'expression est similaire à celle utilisée dans la typologie des vibrations moléculaires.

Dans le dernier cadre évoqué (description des mouvements moléculaires), deux types de degrés de liberté sont identifiés : les degrés de liberté externes au nombre de 6, correspondant aux mouvements de la molécule dans l'espace (translations et rotations), et les degrés de liberté internes, correspondant aux déformations de la molécule par rapport à sa conformation d'équilibre.

Degrés de liberté indépendants

Définition

L'ensemble de degrés de liberté d'un système est indépendant si l'énergie associée avec l'ensemble peut être écrite sous la forme suivante :

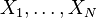
où E_i est une fonction de la seule variable X_i.
Exemple : si X₁ et X₂ sont deux degrés de liberté, et E est l'énergie associée :

• si , alors les deux degrés de liberté sont indépendants.
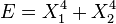
• si , les deux degrés de liberté ne sont pas indépendants. Le terme impliquant le produit de X₁ et X₂ est un terme de couplage, qui décrit une interaction entre deux degrés de liberté.

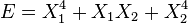
Propriétés

Si est un ensemble de degrés de liberté indépendants alors, à l'équilibre thermodynamique, sont statistiquement indépendants les uns des autres.
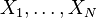
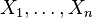
Pour i de 1 à N, la valeur du i^e degré de liberté X_i est distribué selon une loi de Boltzmann. Sa fonction de densité de probabilité est la suivante :

,

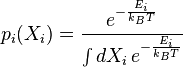
Dans cette section, et par la suite, les indiquent la moyenne de la quantité qu'ils entourent.
L'énergie interne du système est la somme des énergies moyennes associées à chacun des degrés de liberté :

Démonstrations

On postulera par la suite que les échanges d'énergie du système considéré se font avec l'extérieur, et que le nombre de particules du système est constant, c'est-à-dire que l'on se place dans l'ensemble canonique. Rappelons qu'en physique statistique, un résultat qui est démontré pour un système reste vrai pour ce système à la limite thermodynamique dans n'importe quel ensemble. Dans l'ensemble canonique, à l'équilibre thermodynamique, l'état du système est distribué parmi les micro-états selon une distribution de Boltzmann. Si T est la température du système et k_B la constante de Boltzmann, alors la fonction de densité de probabilité associée à chaque micro-état est la suivante :

,

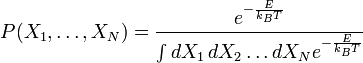
Cette expression se transforme en un produit de termes dépendant d'un simple degré de liberté :

L'existence d'un tel développement de la fonction de densité de probabilité en un produit de fonction d'une seule variable suffit à lui seul à démontrer que les sont indépendants statistiquement les uns des autres.
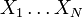
Chaque fonction p_i étant normalisée, il s'ensuit que p_i est la fonction de densité de probabilité du degré de liberté X_i, pour i de 1 à N.
Enfin, l'énergie interne du système est l'énergie moyenne. L'énergie E_i d'un degré de liberté est une fonction de la seule variable X_i. Puisque sont statistiquement indépendantes les uns des autres, les énergies le sont aussi. L'énergie interne totale du système peut être alors écrite comme :