Diagramme horaire - Définition

Distinction v(t) et v(s)

Le problème n'est pas le même sur la route, si on relève

• la vitesse en chaque lieu v(s) ou
• la vitesse à chaque instant v(t).

Cas v(t)

Dans ce second cas (le plus facile), on trace la courbe v(t) de t=0 à to. L'aire sous la courbe donne l'espace parcouru s(to):

Exemple : si la vitesse augmente linéairement v(t) = at, le déplacement sera s(to) = to*ato/2 (aire du triangle rectangle) ; soit s(t0) = 1/2 a to^2 : le mouvement est dit uniformément accéléré.

Cas v(s)

Dans ce cas, on parle de diagramme des espaces : il faut considérer que, pendant un petit chemin ds, le temps dt mis pour le parcourir est dt = ds/v(s). Il faut donc sommer tous les dt pour obtenir la durée du parcours (de s=0 à so). Il faut donc tracer 1/v(s), et prendre l'aire sous la courbe, qui cette fois sera un temps.

Exemple classique : l'aller-retour

Pierre fait le chemin aller de A à B (AB = 10km) à la vitesse de 12km/h. Au retour, plus fatigué, il court à 8 km/h. Question : arrivera-t-il avant ou après Jacques qui court l'aller-retour à 10km/h ?

La réponse est: Pierre arrive après Jacques ; en effet il a couru moins d'une heure à 12km/h et plus d'une heure à 8km/h, donc sa moyenne de vitesse est inférieure à 10km/h.

Ce raisonnement qualitatif est à bien maîtriser : la moyenne harmonique de vitesse est toujours plus petite que la moyenne arithmétique (cf moyenne).

Exemple de Torricelli

v(s) = sqrt( 2gs).

L'aire sous la courbe 1/sqrt(2gs) est sqrt(2so/g), donc le temps de parcours to est tel que s(to) = so = 1/2 g to^2 .

Historiquement, le premier à faire ce calcul est Evangelista Torricelli (de Motu 1641). Il s'agit encore du mouvement uniformément accéléré. Galilée avait hésité à utiliser une courbe qui partait de l'infini au départ. Torricelli, élève d'abord de Castelli, puis de Cavalieri, n'avait pas ces scrupules et a dépassé le Maître.

Exemple relativiste de Bertozzi

Cet exemple est de niveau nettement plus élevé. C'est la modification en relativité restreinte de l'exemple de Torricelli. On ne s'étonnera point que, au début du mouvement, le résultat soit voisin de celui de Torricelli, mais qu'à la fin du mouvement, v reste limitée par la vitesse-limite c.

L'expérience fut réalisée par Bertozzi et donna les résultats escomptés par la relativité restreinte avec une précision remarquable.

v(z) est donnée par l'équation, dite théorème d'énergie cinétique d'Einstein :

On en tire v(z), et il "ne reste plus qu'à faire" les calculs : on conseille d'utiliser la méthode graphique ou numérique; mais ceux qui possèdent plus d'habileté mathématique retrouveront les expressions suivantes :

qui satisfont l'équation précédente dont la solution était unique : c'est donc la bonne (c'est un bon exercice de le vérifier, si on connaît l'opération de dérivation).

Que constater ? si gt/c <<1, v= gt et z = 1/2gt² : Galilée avait raison.

Mais si t devient grand devant c/g, la vitesse v sature à la vitesse-limite c et

 : Einstein a raison : la particule ne peut pas être plus loin que ct.

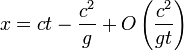
Si on pose la "rapidité" r telle que v = c th r, alors, c'est la rapidité qui croît linéairement r = gT avec le temps "propre" T, ce qui est conforme au principe de relativité galiléenne (il suffit de raisonner à chaque instant t dans le référentiel galiléen tangent : cette solution en effet très élégante est d'Einstein lui-même)

On constate que t = c/g sh gT/c et donc au bout de T = 3c/g , t = ~ c/2g exp gT/c, c’est-à-dire que l'horloge de la particule ralentit énormément T~ c/g Ln (2gt/c)

enfin on peut vérifier que