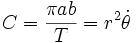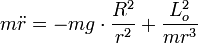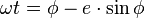Diagramme horaire - Définition
La liste des auteurs de cet article est disponible ici.
Mouvement de Kepler selon Leibniz
C'est un cas très célèbre de mouvement dans un puits de potentiel.
Dès 1689, Leibniz a su comprendre le mouvement radial d'un satellite en écrivant SON équation de l'énergie cinétique (à l'époque, on disait équation des forces vives) :
|
|
Il s'agit donc du mouvement dans un puits de potentiel U(r), si Eo est négative.
Les limites de ce puits s'appellent SP = r minimum = distance périgée et SA = r maximum = distance apogée, racines de l'équation U(r) = Eo.
Soit Lo²/2m (1/r)² - mgR² (1/r) - Eo = 0 , équation du second degré en 1/r :
Leibniz remarqua immédiatement que la demi-somme 1/2(1/SA +1/SP), appelée moyenne harmonique et égale à 1/p est indépendante de Eo (règle 1 de Leibniz), et que la somme (SA +SP) = 2a était indépendante de Lo (règle 2 de Leibniz) : cf mouvement keplerien.
L'équation réécrite avec 2a et p devient :
U(r)/m - Eo/m = Lo²/2m² (1/r² - 2/pr + 1/pa) = -1/2 (dr/dt)².
L'"astuce" usuelle dans ce genre de problème est de considérer la variable phi telle que r= a -c.cosφ , phi variant de 0 à Pi en passant du périgée à l'apogée. Alors l'intégration est beaucoup plus facile, et donne la célèbre équation du temps de Kepler (voir mouvement keplerien:
|
|
En exprimant la fonction réciproque, on obtient phi(t) et donc r(t). (cf mouvement keplerien). Ici ω représente la pulsation du mouvement périodique dans le puits. On retrouve la troisième loi de Kepler :
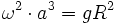
L'équation donnant l'angle polaire se trouve via l'intégration de la deuxième loi de Kepler :