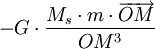Mouvement keplerien - Définition

Introduction

En astronomie, le mouvement keplerien basé sur les trois lois de Kepler ne donne que peu d'indications sur le mouvement des planètes. Cet article se veut un approfondissement complémentaire.

Quelques éléments de base

Données culturelles

Les connaissances astronomiques du monde gréco-romain sont résumées par Ptolémée (+ 200 JC), transmises et améliorées par l'Empire byzantin sous le nom de « Trismegistie » (le livre du Maître), par l'Empire arabe sous le nom de l'Almageste.

Copernic (1543) fait publier le « système héliocentrique » à sa mort.

Kepler (1571-1630), grâce à l'analyse soigneuse des observations précises de son maître Tycho Brahe (1541-1601), publie ses trois célèbres lois (Cf. Lois de Kepler) en 1609, 1611, 1618. (Comme 1618 marque le début de la Guerre de Trente Ans, le reste de sa vie sera troublé).

Newton (1642-1727), certainement le scientifique le plus connu avec Einstein, démontre ces lois en 1687 (Cf. Philosophiae Naturalis Principia Mathematica ; Démonstration des lois de Kepler) : c'est le début d'une nouvelle ère : la mécanique céleste et la mécanique classique fondées sur le Calculus (Cf. Principia et Calculus).

Newton y ose braver un interdit : la notion d'action instantanée à distance ; la gravitation agit instantanément en 1/r². C'est le célèbre « hypotheses non fingo ». La « résistance cartésienne », plus la très grande difficulté mathématique des Principia provoquera un temps de réception assez long de son oeuvre, et il faudra attendre les ouvrages d'Euler, de McLaurin et de Clairaut, pour éclaircir la situation. Néanmoins les plus grands esprits de l'époque (Huygens, Leibniz, etc ...) reconnaissent immédiatement la portée des Principia.

La constante de Gravitation sera évaluée par Cavendish en 1785 : G = 6.67 10^-11 N.m²/kg². (Il y a une très grande différence expérimentale entre trouver GM, ce qui est facile, et tester la loi de Newton en mesurant G : cela est encore l'objet de recherches de nos jours (2007)).

Masse inerte et masse grave sont confondues, ce qui explique la loi de Galilée : indépendance dans la chute libre du corps pesant & inerte : fer ou plume tombent (gravitent) de même façon ! Elevée au rang de Principe d'Equivalence par Einstein en 1915, elle sera un des fondements de la Relativité Générale qui redonne une loi de Newton « corrigée » : il y a action à distance mais non instantanée (via une « distorsion de l'espace-temps », pour le dire vite ! ). (Les lois d'Einstein sont toujours sur « le grill », surtout depuis les récentes données du satellite W-map : énergie noire et matière noire sont l'essentiel de notre Univers ; autant avouer notre mauvaise compréhension actuelle de l'Univers, ceci vraisemblablement parce que la théorie quantique des équations d'Einstein n'a toujours pas été trouvée, malgré un intense travail théorique).

Données mathématiques de base

La géométrie de l'ellipse est essentielle dans l'étude du mouvement keplerien.

On rappelle que :

•  := paramètre ou demi-lactus-rectum en latin et

•  := excentricité

•  := le demi grand axe

•  := le demi petit axe

•  := la distance du foyer au centre.

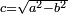
Voir l'article Ellipse (mathématiques)#Rapport entre les grandeurs pour les relations entre ces grandeurs.

Une ellipse de jardinier ( ) s'écrit en cartésiennes :

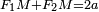
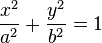
C'est l'affine d'un cercle : et .

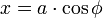
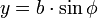
En coordonnées polaires, F étant pris pour origine, et la direction péricentrique comme axe de base : FM := .

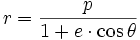
Donc r augmente quand θ augmente de 0 à π :

• θ = 0 [ ]

• [ r = p ]

• [ r = FB = a ]

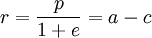
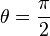
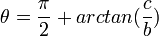
• θ = π [r = FA = ]

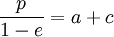
On pourra consulter l'article (conique, discussion), pour une présentation plus géométrique, centrée sur le problème de Kepler.

Données physiques de base

Le Soleil S exerce sur la planète T

la force centripète

et donc (m disparaît : loi de Galilée).

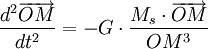
La force étant en , l'énergie potentielle par unité de masse est (+ 0, convention dite à l'infini).

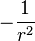
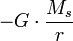
[Dans le cas des satellites artificiels de la Terre, on remplace -> , et l'énergie potentielle massique est .

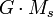
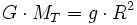
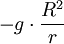
La deuxième vitesse cosmique est donc .

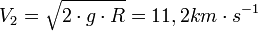
La première vitesse cosmique est , correspondant à une orbite circulaire basse altitude de 84 minutes, soit environ 17 tours en 1 jour].

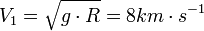
Comme on l'a souligné ou sont très bien connus ( environ onze chiffres significatifs) mais pas G !

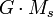
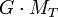
Conséquences de base

Le mouvement est donné une fois TMo et Vo données (6 paramètres) : c'est le Principe Fondamental de la Dynamique classique. Mais ces deux vecteurs définissent un plan (s'ils ne sont pas colinéaires, ce qui sera supposé dans la suite par souci de simplification). La solution du problème étant unique, le principe de symétrie (dit de Curie) montre que la trajectoire doit être dans ce plan (disons z = 0). Donc en fait le problème, comme dans tous les problèmes dits de champ central, est à quatre paramètres réels et non six : deux paramètres donnent la trajectoire à une isométrie près : exemples : (a et b) ou (p et e), etc. Et il en faudra un de plus pour la donnée de l'isométrie (la position du périgée en général) et un de plus pour la date de passage au périgée (ce qui fait bien quatre paramètres).

Convention d'unités

Comme on a vu ( loi de Galilée) que le problème ne dépendait pas de la masse, il est usuel de se référer à une masse unité : parfois on change de lettre, parfois non ( cf analyse dimensionnelle ).

Ainsi le moment cinétique se calcule aisément Lo, et C : = Lo/m en m²/s désigne la vitesse aréolaire. Comme on ne peut distinguer la droite de la gauche, donc le sens de parcours de la planète, ce sera toujours C² qui interviendra ( en m²(m/s)² ).

De même l'énergie Eo (négative)( en joule) sera notée Eo' = Eo/m ( en vitesse*vitesse soit en (m/s)².

Enfin le paramètre GM est souvent rassemblé en une lettre k (pour dire cste de Gauss ?) en m. (m/s)²

Ainsi, il apparaît immédiatement que le problème reformulé ainsi est un problème uniquement de cinématique, bien que souvent il soit enseigné comme un problème de dynamique : c'est une confusion assez naturelle, mais dans tous les problèmes où la loi de Galilée s'applique, la masse disparaît ; tous les corps, pierre ou plume, tombent (dans le vide) de la même façon, aussi contre-intuitif que cela puisse paraître.

Le mouvement keplerien étant périodique, on appelle souvent T la période de révolution et la pulsation ou cadence en rad/s du mouvement. Si on choisit T comme unité de temps ( cela a été la norme internationale du S.I. de 1951 à 1961), alors k et ω définissent le système d'unités naturel du problème : en particulier, l'unité de longueur est souvent nommée a :

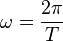
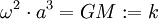
est la célèbre formule de 1618 que les lycéens apprennent.

- - -

Alors, une fois acquis ces préalables, il est démontré dans l'article Lois de Kepler que la géométrie de l'ellipse est donnée par :

• le grand axe 2a : = f(C^2, Eo', k) ne dépend pas de C ! et est donc le monôme -k/E'o) *cste (Cf. le théorème PI) : cette cste vaut 1 :

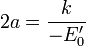
(calculable aisément via le cas d'une trajectoire circulaire)

• le paramètre p, lui, ne dépend pas de Eo et est donc le monôme C²/k * cste : la cste vaut 1 :

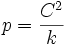
(formule calculable aisément aussi via le cas circulaire)

• le vecteur excentricité e (vecteur de Runge-Lenz) :

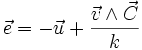
Il est constant, dirigé vers le périgée et de module e, l'excentricité et donc :

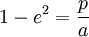
Les trois lois de Kepler et ces trois formules permettent de comprendre la plupart des problèmes, (en particulier les problèmes de balistique extérieure et ceux des satellites artificiels).

Remarque : les valeurs de a et p viennent rapidement de Leibniz (1689) par l'intermédiaire de « son » théorème de l'énergie cinétique :

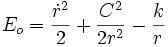
où le terme désigne la barrière centrifuge,

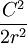
ce qui correspond à une équation différentielle de Newton, dite de Leibniz :

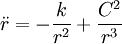
qui a été étudiée en cinématique (Cf. diagramme horaire, mouvement de Leibniz).

L'importance du vecteur excentricité fût soulignée par Hermann (1710 & 1713)), redécouverte par Laplace, puis réutilisée par Runge et Lenz (Cf. vecteur de Runge-Lenz). Elle a fait couler des flots d'encre, et continue à le faire.