Dimension de Krull - Définition

Dimension d'un anneau

Si A est un anneau commutatif unitaire, sa dimension de Krull est par définition la dimension de Krull de SpecA.

Exemples

• Si A est intègre, alors dimA = 0 si et seulement si A est un corps.

• Un anneau noethérien est de dimension 0 si et seulement si c'est un anneau artinien.

• Les anneaux de Dedekind sont de dimension 0 pour les corps et 1 pour les autres.

• Si A est noethérien de dimension finie, alors est de dimension n + dimA.

Dimension des variétés algébriques

• Théorème Soit X une variété algébrique intègre sur un corps K. Alors la dimension de X est égale au degré de transcendance sur K du corps de fonctions rationnelles de X.

• La dimension du produit fibré de deux variétés algébriques sur K est la somme des dimensions.

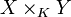
• Une courbe sur K est une variété algébrique dont les composantes connexes sont de dimension 1. On a vu ci-dessus qu'une hypersurface V(f) dans le plan affine est une courbe. L'inverse n'est pas toujours vraie même si la courbe est affine et non-singulière.

Intuition

La variété algébrique affine sur un corps k est de dimension n. Lorsque k est algébriquement clos, l'espace sous-jacent de cette variété est kⁿ qui est un espace affine de dimension (linéaire) n. La dimension d'une hypersurface dans (c'est-à-dire l'ensemble des zéros d'un polynôme non constant) est n − 1. En particulier, l'ensemble des zéros d'un polynôme à deux variables est de dimension 1 (une courbe algébrique).

Sur le corps des réels, les points réels d'une variété algébrique de dimension n sans point singulier forment une variété différentielle de dimension n (ou vide si la variété algébrique n'a pas de point réel comme la courbe x² + y² + 1 = 0).

Sur le corps des nombres complexes, toute variété algébrique peut être vue comme un espace analytique complexe. Les dimensions algébriques et analytiques complexes coincident.