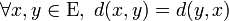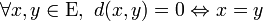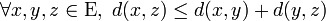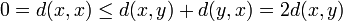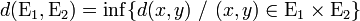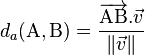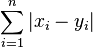Distance (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une distance est une application qui formalise l'idée intuitive de distance, c'est-à-dire la longueur qui sépare deux points. C'est par l'analyse des principales propriétés de la distance usuelle que Fréchet introduit la notion d'espace métrique, développée ensuite par Hausdorff. Elle introduit un langage géométrique dans de nombreuses questions d'analyse et de théorie des nombres.
À partir de la définition d'une distance, vue comme une application satisfaisant à certains axiomes, d'autres notions de distance peuvent être définies, comme par exemple la distance entre deux parties, ou la distance d'un point à une partie, sans que ces dernières répondent à la définition première d'une distance.
Distance sur un ensemble
Définition
En mathématiques, on appelle distance sur un ensemble E une application
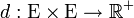
| Nom | Propriété |
|---|---|
| symétrie |
|
| séparation |
|
| inégalité triangulaire |
|
Un ensemble muni d'une distance s'appelle un espace métrique.
Remarque
Dans la définition d'une distance, on demande généralement que l'ensemble d'arrivée soit
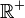

en utilisant respectivement la séparation, l'inégalité triangulaire puis la symétrie.
Propriété : Ultramétrie
La distance est dite ultramétrique si de plus :
| Nom | Propriété |
|---|---|
| Ultramétrie |
Un exemple de telle distance intervient de façon cruciale dans la théorie des valuations p-adiques. L'interprétation géométrique de l'inégalité triangulaire dans un espace ultramétrique amène à dire que tous les triangles sont isocèles.
Distance entre deux ensembles
Soient E1 et E2 deux parties d'un espace métrique muni d'une distance d, on définit la distance entre ces deux ensembles comme :
- N.B.
- Cette « distance » n'est pas une distance sur l'ensemble des parties de E au sens des axiomes définis plus haut. En particulier si la distance entre deux ensembles est nulle, on ne peut pas en déduire que ces ensembles sont égaux.
Néanmoins, il est possible de définir une vraie distance entre les parties compactes d'un espace métrique. Pour cela, voir : distance de Hausdorff.
Distance algébrique
Soit deux points A et B d'un espace affine par lesquels passe une droite orientée (une droite munie d'un sens, c'est-à-dire engendrée par un vecteur

- sa valeur absolue soit la distance (définie ci-dessus) entre A et B
- si la valeur est non nulle :
- le réel soit positif dans le cas où le vecteur
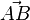

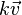
- négatif sinon.
- le réel soit positif dans le cas où le vecteur
On peut démontrer que la distance algébrique de A vers B (notée da(A,B)) vaut :
Attention, la distance algébrique n'est pas une distance, puisqu'elle est non-symétrique :
- da(A,B) = − da(B,A)
Distance sur des espaces vectoriels
Dans un espace vectoriel normé
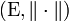
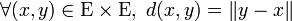
En particulier, dans

| Nom | Paramètre | Fonction |
|---|---|---|
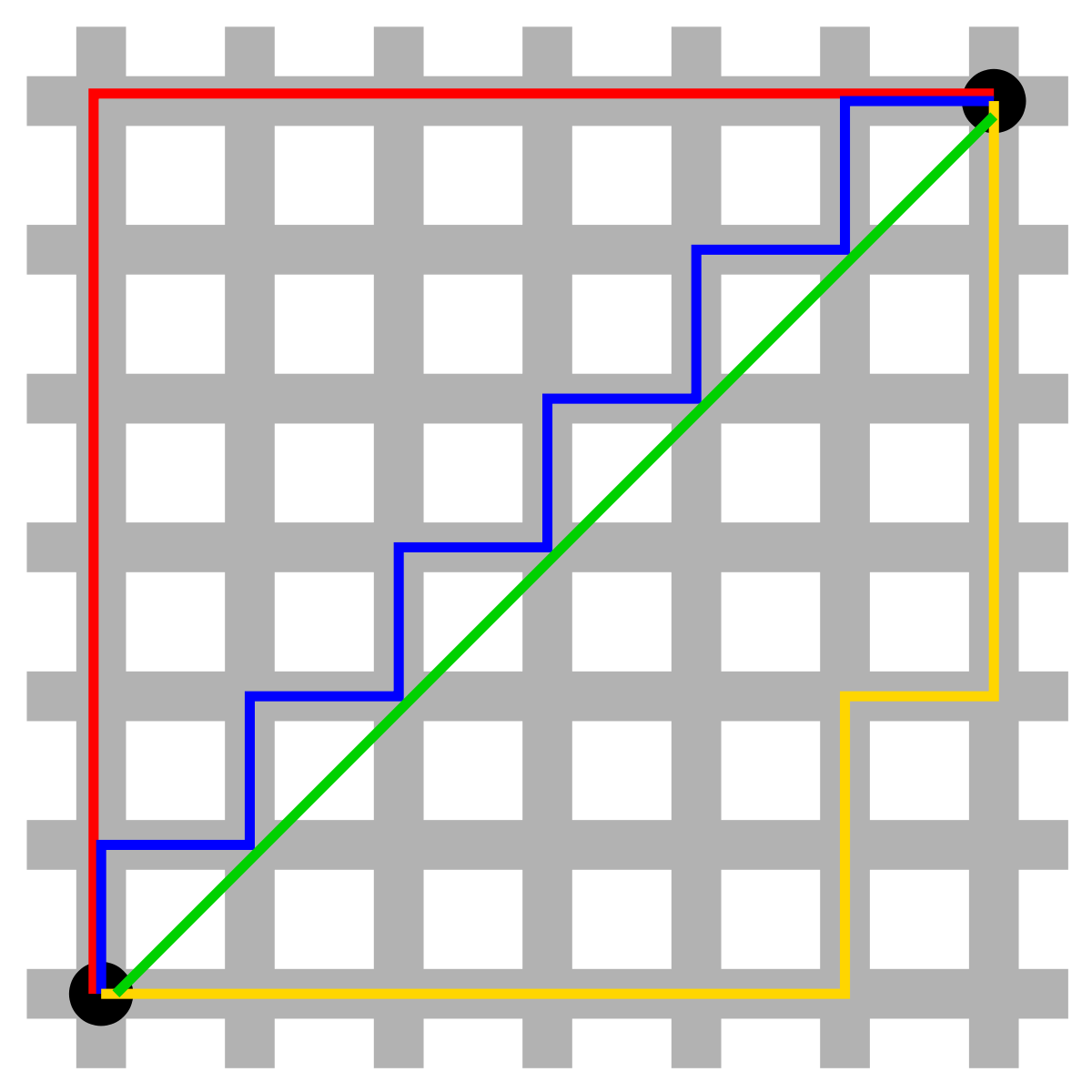
| distance de Manhattan | 1-distance |
|
| distance euclidienne | 2-distance |
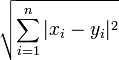
|
| distance de Minkowski | p-distance |
![\sqrt[p]{\sum_{i=1}^n |x_i-y_i|^p}](https://static.techno-science.net/illustration/Definitions/autres/c/c7059cf186b2bfabb5ff2e1eb2ffb15d_afdaf5e68378ff7b832741f38e0f8c0d.png)
|
| distance de Tchebychev | ∞-distance |
![\lim_{p \to \infty}\sqrt[p]{\sum_{i=1}^n |x_i-y_i|^p} = \sup_{1 \leq i \leq n}{|x_i-y_i|}](https://static.techno-science.net/illustration/Definitions/autres/e/eb54f4bd88bb99057ed88359a6a19cc9_b12d2664a2c52c51850bc0ee0667dede.png)
|
La 2-distance permet de généraliser l'application du théorème de Pythagore à un espace de dimension n. C'est la distance la plus intuitive.
La p-distance est rarement utilisée en dehors des cas p = 1, 2 ou ∞. La 1-distance présente la particularité amusante de permettre la définition en toute rigueur de sphères carrées (voir oxymore).