Distance (mathématiques) - Définition

Distance d'un point à une partie

On peut particulariser la définition précédente en prenant l'un des deux ensembles réduit à un point.
Si A est une partie non-vide d'un espace métrique E, et si x est élément de E, on définit la distance de x à A par:

.

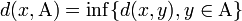
C'est le rayon de la plus grande boule ouverte de centre x qui ne rencontre pas A.

On prendra garde au fait que n'implique pas que x soit élément de A. Par exemple, dans muni de la valeur absolue, la distance de 0 à l'intervalle ouvert ]0,1[ est nulle, ou la distance de tout réel à l'ensemble des rationnels est nulle également.
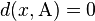
On peut démontrer plus précisément que la distance de x à A est nulle si et seulement si x est un point adhérent à A.

L'application vérifie l'inégalité triangulaire:

.

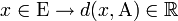
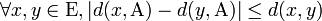
C'est donc une application continue, puisque 1-lipschitzienne.

Distances entre deux permutations

Il est également possible de définir des distances entre des permutations. L'exemple suivant est très utilisé dans le réarrangement de génomes. Soit S un ensemble de permutations modélisant diverses opérations; alors la distance entre deux permutations π et σ est la longueur d'une séquence minimale formée du produit d'éléments de S telle que cette séquence transforme π en σ.

Ces distances peuvent également servir à mesurer, de diverses manières, le désordre présent dans une séquence. On utilise alors ces mesures pour analyser les performances de divers algorithmes de tri, ou pour construire de nouveaux algorithmes de tri qui effectuent un nombre de comparaisons optimal par rapport à la mesure de désordre choisie. L'algorithme de Levenshtein mesure une telle similarité.

Distance sur une sphère

• Voir : Distance du grand cercle