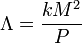Élimination du voisinage - Définition

Introduction

Dans les phases finales de la formation des planètes selon l'hypothèse nébulaire, une planète doit avoir éliminé son voisinage sur sa propre zone orbitale, ce qui signifie que, du point de vue de la gravitation, elle est devenue dominante et qu'il n'existe aucun autre corps de taille comparable hormis ses propres satellites naturels ou bien les corps qui sont placés d'une façon quelconque sous son influence gravitationnelle. Actuellement, la définition des planètes adoptée par l'Union astronomique internationale (UAI) ne comprend que les corps qui ont éliminé le voisinage de leur orbite.

Un gros corps céleste qui respecte les autres critères d'une planète, mais qui n'a pas éliminé son voisinage est classé comme une planète naine. Ceci concerne Pluton qui partage son voisinage orbital avec les objets de la ceinture de Kuiper tels que les plutinos. La définition de l'UAI ne lie aucun nombre ni aucune équation spécifiques à ce terme, mais l'étendue sur laquelle toutes les planètes ont éliminé leur voisinage est bien supérieur à celui de n'importe quelle planète naine ou de n'importe quelle candidate connues à ce jour.

La phrase dérive peut être d'un article présenté à l'Assemblée Générale de l'UAI en 2000 par Alan Stern et Harold F. Levison (en). Les auteurs ont utilisé plusieurs phrases similaires pour développer une base théorique de détermination si un objet en orbite autour d'une étoiles est susceptible d'avoir éliminé la region avoisinante des planétésimaux, en se basant sur la masse de l'objet et sur sa période orbitale.

Il était devenu nécessaire de clarifier la distinction entre planètes, planètes naines et autres planètes mineures parce que l'UAI avait adopté différentes règles pour designer les nouvelles planètes et les planètes mineures, récemment découvertes, sans formaliser la base pour les distinguer. Le processus de désignation pour Eris 'casée' après l'annonce de sa découverte en 2005, mettait en suspens la clarification de cette première étape.

Détails

La phrase se réfère à un corps en orbite (une planète ou une protoplanète qui essuierait sa région orbitale au cours du temps, par interaction gravitationnelle avec des corps de taille inférieure situés à proximité. Après de nombreux cycles orbitaux, un gros corps tendra à influer sur de plus petits, soit par accrétion avec lui-même, ou par répulsion vers une autre orbite. En conséquence, il finit par ne plus partager la région de son orbite avec aucun autre corps de dimensions significatives par rapport aux siennes propres, à l'exception de ses propres satellites, ou des corps gouvernés par sa propre influence. Cette dernière restriction exclue toutefois les objets dont l'orbite peut croiser la sienne, mais avec lesquels il ne peut pas entrer en collision du fait de la résonance orbitale, tels que Jupiter et ses satellites Troyens, la Terre et (3753) Cruithne ou Neptune et les plutinos.

Steven Soter (en) du Départment d'Astrophysique, au Museum américain d'Histoire Naturelle, a écrit qu'un corps héliocentrique avec Λ > 1 [viz. une planète] a éliminé une fraction substantielle des petits corps de son voisinage orbital. Λ (Lambda) est un paramètre proposé par Stern et Levinson qui mesure l'ampleur à laquelle, sur une longue période, un corps éparpille les masses inférieures à l'extérieur de sa zone orbitale. Mathématiquement, Λ est défini comme :

où k est approximativement constant, et M et P sont respectivement les masses et les périodes orbitales des corps éparpillés. Deux corps se définissent comme partageant une zone orbitale si leurs orbites traversent un distance radiale commune au corps primaire, et leur période non-résonnante diffère de moins d'un ordre de magnitude. La similarité de l'ordre de magnitude dans les exigences relatives à la période exclue les comètes du calcul, mais la masse combinée des comète se révèle de toute façon négligeable par rapport à celle des autres 'petits corps du Système solaire', de telle sorte que leur inclusion aurait eu peu d'impact sur les résultats. Stern et Levinson ont trouvé une différence de cinq ordres de grandeur de magnitude dans Λ entre la plus petite planète tellurique et les astéroïdes les plus gros et les KBOs (objets de la Ceinture de Kuiper).

Soter a poursuivi en proposant un paramètre qu'il a baptisé discriminant planétaire, désigné par le symbole µ (mu), qui représente une mesure expérimentale du degré réel de nettoyage de la zone orbitale. µ se calcule en divisant la masse du corps candidat par la masse totale des autres objets qui partagent sa zone orbitale.

Voici une liste des planètes par ordre décroissant de discriminant planétaire, définie par Steven Soter, où le discriminant μ est le rapport entre la masse des corps et la masse totale des autres corps non-résonants et non-satellitaires dans la même zone orbitale, également définie par Soter. Figurent aussi le paramètre Λ, le rapport du carré de la masse sur la période orbitale, normalisé par rapport aux valeur de la Terre (Λ/Λ_E). (Noter que Λ_E ~ 1.5^e, de façon que les valeurs non normalisées de Λ pour les huit planètes définies par l'UAI sont des ordres de magnitudes supérieurs à 1, et les valeurs de Λ pour les planètes naines sont des ordres de magnitudes inférieurs à 1.).