Épicycle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L’épicycle est un composant essentiel du système astronomique de Ptolémée (IIe siècle) (système géocentrique qui sera utilisé jusqu'à Copernic (XVIe siècle) au moins).
Histoire du concept
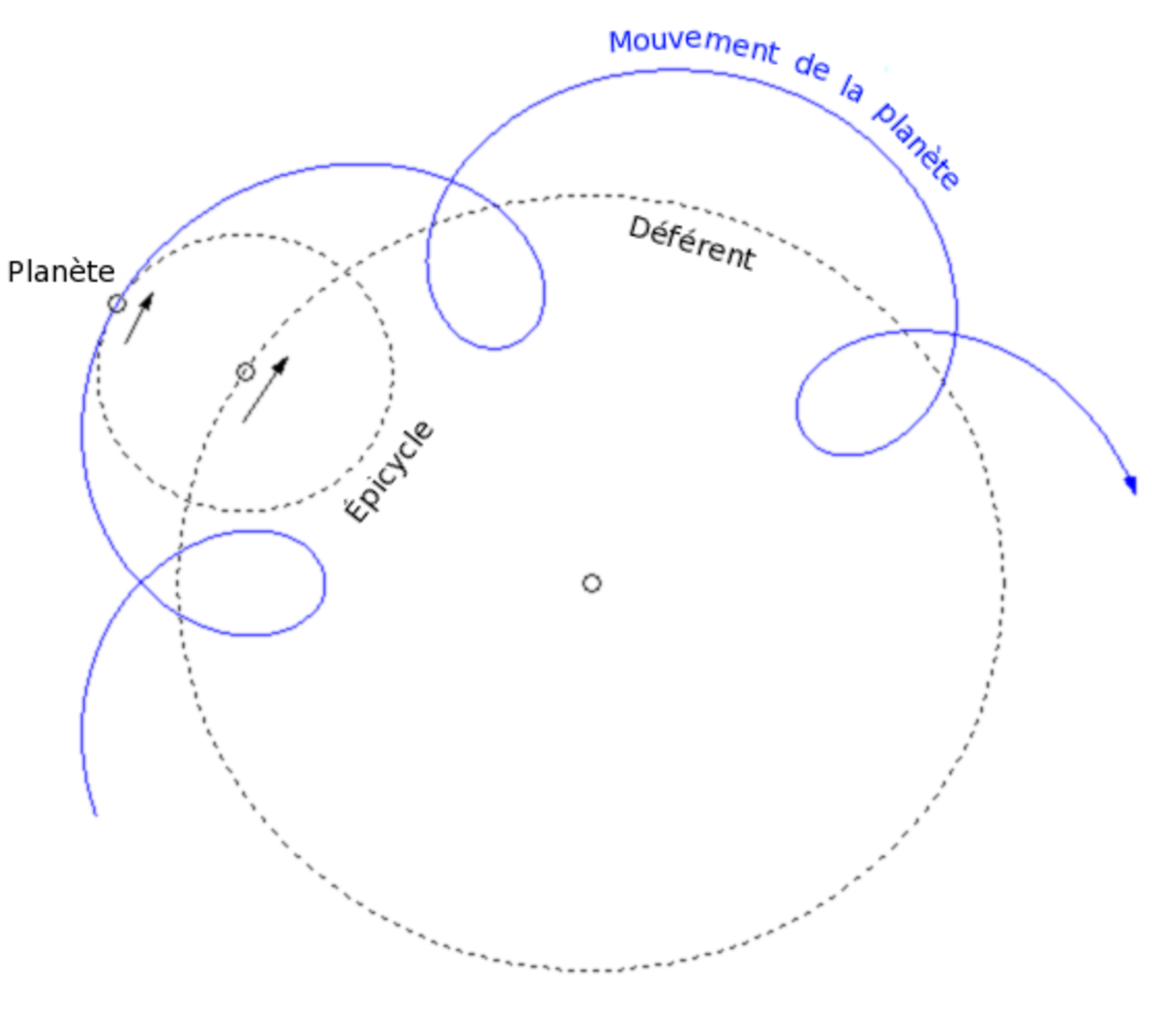
Pour expliquer notamment les mouvements des planètes (ou astres errants), qui semblent parfois rétrograder, les astronomes grecs, dont Hipparque (IIe siècle av. J.-C.) introduisirent l'épicycle : il s'agit d'un cercle dont le centre décrit un cercle appelé déférent, qui (dans la première ébauche du système en tout cas) est centré sur la Terre. Ce système remplace progressivement celui des "sphères homocentriques" d'Eudoxe de Cnide, qui avait la faveur d'Aristote (IVe siècle av. J.-C.) mais qui supposait à tort que les planètes étaient à une distance constante de la Terre.
L'élaboration de ce système constitue un progrès capital dans l'astronomie antique. En décomposant les mouvements complexes des astres en cercles parcourus par ceux-ci à vitesse constante, on rendait possible la confection de tables astronomiques très précises et très fiables. Ces tables permettront, par exemple, les premiers calculs d'éclipse solaire. Dès lors, la théorie géocentrique avait beau être fausse, elle fonctionnait. La théorie des épicycles ne sera donc plus remise en question jusqu'à Copernic. Cependant, si cette théorie est commode pour décrire les mouvements apparents du Soleil et de la Lune, elle mène à des constructions très complexes pour les planètes, et ces constructions se complexifient chaque fois qu'on veut affiner la description de leurs mouvements.
Ainsi, l'introduction de l'équant par Ptolémée (IIe siècle) permet d'améliorer le modèle, notamment en rendant mieux compte des vitesses apparentes des planètes.
Copernic (XVIe siècle) dénonça ces outils mathématiques, si nombreux qu'ils avaient rendu l'astronomie trop complexe pour qu'elle prétende réellement rendre compte de la réalité. A l'image de Dieu, la réalité devait être plus simple. De plus, les "mathématiciens" n'étaient pas tous d'accord entre eux et ne réussissaient pas à prévoir parfaitement les mouvements des planètes. Son système héliocentrique aura donc comme vocation aussi, de simplifier l'astronomie de son époque. En plaçant le Soleil au voisinage du centre du monde (chez Copernic le centre du Cosmos n'est pas dans le Soleil comme dans les premiers travaux de Kepler, mais au centre de l'orbite terrestre...), il n'y avait plus besoin par exemple de certains épicycles pour rendre compte des rétrogradations des planètes. Mais au final, le système de Copernic restait tout de même très complexe, les trajectoires des planètes restant circulaires donc inaptes à rendre compte des mouvements apparents des planètes de manière suffisamment précise.
Kepler (XVIIe siècle) argumenta différemment contre les épicycles. Dans les quelques chapitres qui débutent son ouvrage de référence, l'Astronomia Nova (publié en 1609), il explique dans sa logique de forces physiques permettant au Soleil de pousser littéralement les planètes sur leurs orbites, que les épicycles doivent être considérés comme des artifices mathématiques. Ils n'ont aucune réalité, notamment parce que le centre mathématique d'un cercle (qu'il soit en mouvement ou non), ne saurait constituer un centre de force (entraînant la planète sur un nouveau cercle) ni un support pour la force issue du Soleil. C'est donc le corps de la planète elle-même qui doit être entraîné par une telle force. Kepler continua donc un temps d'utiliser les épicycles ou des artifices mathématiques s'en rapprochant, mais en les considérant seulement comme le moyen de modéliser les effets de forces physiques (motrices puis magnétiques) en jeu pour lui dans le système solaire. On ne saurait imaginer à quel point son approche physique fut révolutionnaire pour l'époque. Même Galilée qualifia de puérile l'idée d'une force (que Kepler appliquait aussi à la Lune) qui agirait directement sur les eaux de la Terre pour provoquer les marées... Auparavant l'astronomie était exclusivement mathématique, la question des fondements étant réservée aux théologiens sous peine d'excommunication. C'est pourquoi aussi les épicycles ont pu perdurer si longtemps.

















































