Espace anti de Sitter - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et en physique, l'espace anti de Sitter n-dimensionnel, noté AdSn, est l'analogue lorentzien de l'espace hyperbolique n-dimensionnel. Il est pourvu d'une symétrie maximale et est une variété lorentzienne avec une courbure scalaire négative constante.
Dans le langage de la relativité générale, l'espace anti de Sitter est une solution de vide à l'équation de champ d'Einstein avec une constante cosmologique Λ négative.
L'espace anti de Sitter est la courbure analogue négative de l'espace de Sitter, nommée ainsi en l'honneur de Willem de Sitter. Il est utilisé dans la correspondance AdS/CFT.
Définitions et propriétés
L'espace anti de Sitter peut être défini comme une sous-variété de R2,n − 1 en codimension 1. Prenons l'espace R2,n − 1 avec la métrique standard :
-
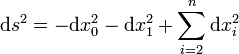
L'espace anti de Sitter est la sous-variété décrite par l'hyperboloïde
où α est une sorte de constante non-nulle avec des dimensions de longueur. La métrique sur l'espace anti de Sitter est la métrique induite par la métrique ambiante. On peut vérifier qui la métrique induite n'est pas dégénérée et a la signature lorentzienne.
L'espace anti de Sitter peut aussi être défini comme le quotient O(2,n − 1) / O(1,n − 1) de deux groupes orthogonaux indéfinis, ce qui montre que c'est un espace symétrique non-riemannien.
L'espace de Sitter n-dimensionnel a O(n − 1,2) comme groupe isométrique. Il n'est pas simplement connexe ; il est homéomorphe au produit
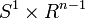
L'espace anti de Sitter comme espace homogène et symmétrique
De la même manière que la sphère
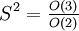
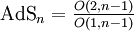
-
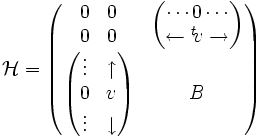
où B est une matrice diagonale symétrique. Une complémentarité dans l'algèbre de Lie de
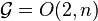
-
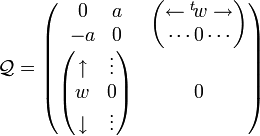
Ces deux
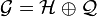
![[\mathcal{H},\mathcal{Q}]\subseteq\mathcal{Q}, \quad [\mathcal{Q},\mathcal{Q}]\subseteq\mathcal{H}](https://static.techno-science.net/illustration/Definitions/autres/f/fa68d7c0d7be0c27b4ec2297d7467be7_f29f71497489dc6ccf1cdbd4fd8d868b.png)