Algèbre de Lie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une algèbre de Lie, nommée en l'honneur du mathématicien Sophus Lie, est un espace vectoriel qui est muni d'un crochet de Lie bilinéaire, antisymétrique et qui vérifie l'identité de Jacobi. Une algèbre de Lie est un cas particulier d'algèbre sur un corps.
Définitions, exemples et premières propriétés
Définition
Soit

Une algèbre de Lie sur

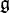

![(x,y) \mapsto [x,y]](https://static.techno-science.net/illustration/Definitions/autres/7/75e87350f83275e11f126171780fd7ca_e9e2b5b56a7683ea300b25f07bb6a19b.png)
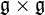
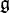
-
![\forall x \in \mathfrak{g},\ [x,x]=0](https://static.techno-science.net/illustration/Definitions/autres/f/f3223a3fe063412bb2f5033ba34850f5_05528a82abf981144bc149b296353746.png)
-
![\forall x,y,z \in \mathfrak{g},\ [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0](https://static.techno-science.net/illustration/Definitions/autres/6/67d115952cf9c1c691b6053868febb0d_e64df769790e9e63a087617d8dde53a7.png)
Le produit [x,y] est appelé crochet de Lie (ou simplement crochet) de x et y. Puisque le crochet est une fonction bilinéaire alternée de x,y, on a aussi l'identité [x,y] = − [y,x] pour tous x,y dans
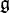
Une sous-algèbre de Lie de
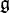
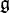
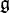

Remarque : contrairement aux algèbres tensorielles (et aux algèbres de Clifford, dont les algèbres extérieures), les algèbres de Lie ne sont pas unitaires, ni associatives.
Quelques exemples classiques d'algèbres de Lie
- Tout espace vectoriel E peut être muni d'une structure d'algèbre de Lie, en posant
![\forall x,y \in E,\ [x,y]=0](https://static.techno-science.net/illustration/Definitions/autres/4/47b2e0b6393e77c2e6376834f8c87276_bd185b95392a3c1231b4930146d48a9d.png)
- On peut, à partir d'une algèbre associative (A, * ) , construire une algèbre de Lie, de la façon suivante : on pose
![\forall x,y \in A,\ [x,y]=x*y-y*x](https://static.techno-science.net/illustration/Definitions/autres/5/59711ef28af13f749a361b567295a858_6ac109c982c8d5297b0d88679364ff9c.png)
- Inversement, toute algèbre de Lie
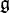
- Inversement, toute algèbre de Lie
- Comme exemple concret de la situation ci-dessus, considérons
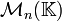
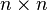

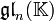
- Bien évidemment, tout sous-espace vectoriel de
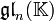
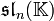
- Un autre exemple fondamental, plus géométrique, est le suivant. Soit M une variété différentielle. Alors l'espace vectoriel formé par les champs de vecteurs sur M possède une structure naturelle d'algèbre de Lie, sans être une algèbre.
- En particulier, l'ensemble des vecteurs de Killing d'une variété forme une algèbre de Lie, qui correspond au groupe d'isométries de la variété considérée.
- L'espace euclidien tri-dimensionnel

Morphismes et idéaux
Un morphisme d'algèbre de Lie
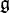
-
![\forall a,b \in \mathfrak{g},\ \phi([a,b])=[\phi(a),\phi(b)]](https://static.techno-science.net/illustration/Definitions/autres/7/79fe9d02198bb8da7ba2c3fe5df52add_92685eaf0597dc693b7ab8a79d516d0f.png)
Un idéal de
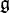
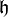
![\forall g\in\mathfrak{g},\ \forall h\in \mathfrak{h},\ [g,h]\in\mathfrak{h}](https://static.techno-science.net/illustration/Definitions/autres/9/9fe5cc6e32f7a61a988f42d549cb43b3_5e9972f795c28334024626d6fa538cd5.png)
Si
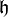
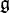
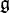
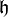
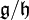
![[g+\mathfrak{h},g'+\mathfrak{h}] = [g,g']](https://static.techno-science.net/illustration/Definitions/autres/8/82d29f5c4eb7af6feb2661af74a7bd29_18901d9a4535358c0912611c8efed98e.png)
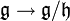
Une représentation d'une algèbre de Lie
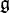
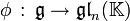
Le morphisme
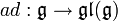
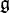
![Z(\mathfrak{g})=\{g\in\mathfrak{g}\forall h\in\mathfrak{g} [g,h]=0\}](https://static.techno-science.net/illustration/Definitions/autres/a/afe7160b530a847134d5f4291027ee9c_0785c54d5af87b310826ded99beacfe5.png)