Relativité générale - Définition

Introduction

Avant Einstein

Avec Einstein

En physique des particules

Méta

La relativité générale, fondée sur le principe de covariance générale qui étend le principe de relativité aux référentiels non-inertiels, est une théorie relativiste de la gravitation, c'est-à-dire qu'elle décrit l'influence sur le mouvement des astres de la présence de matière et, plus généralement d'énergie, en tenant compte des principes de la relativité restreinte. La relativité générale englobe et supplante la théorie de la gravitation universelle d'Isaac Newton qui en représente la limite aux petites vitesses (comparées à la vitesse de la lumière) et aux champs gravitationnels faibles.

La relativité générale est principalement l'œuvre d'Albert Einstein, dont elle est considérée comme la réalisation majeure, qu'il a élaborée entre 1907 et 1915. Les noms de Marcel Grossmann et de David Hilbert lui sont également associés, le premier ayant aidé Einstein à se familiariser avec les outils mathématiques nécessaires à la compréhension de la théorie (la géométrie différentielle), le second ayant franchi conjointement avec Einstein les dernières étapes menant à la finalisation de la théorie après que ce dernier lui eut présenté dans le courant de l'année 1915 les idées générales de sa théorie.

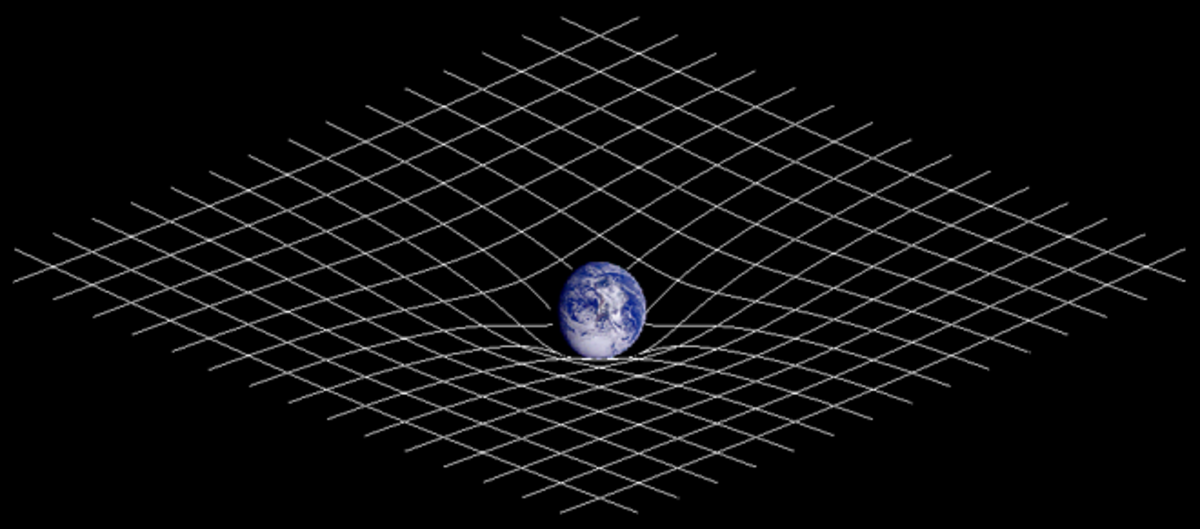
La relativité générale est fondée sur des concepts radicalement différents de ceux de la gravitation newtonienne. Elle énonce notamment que la gravitation n'est pas une force, mais est la manifestation de la courbure de l'espace (en fait de l'espace-temps), courbure elle-même produite par la distribution de matière. Cette théorie relativiste de la gravitation donne lieu à des effets absents de la théorie newtonienne mais vérifiés, comme l'expansion de l'Univers, ou potentiellement vérifiables, comme les ondes gravitationnelles et les trous noirs. Aucun des nombreux tests expérimentaux effectués à ce jour (2009) n'a pu la mettre en défaut, à l'exception possible de l'anomalie Pioneer qui pourrait être la première indication d'un écart entre les phénomènes observés et la relativité générale, quoique d'autres interprétations de ce phénomène soient envisageables.

Généralités

Nécessité d'une théorie relativiste de la gravitation

Représentation bidimensionnelle de la distorsion spatio-temporelle. La présence de matière modifie la géométrie de l'espace-temps.

La théorie de la gravitation universelle proposée par Newton à la fin du XVII^e siècle se fonde sur la notion de force de gravitation agissant selon le principe d'action à distance, c'est-à-dire le fait que la force exercée par un corps (par exemple le Soleil) sur un autre (la Terre) est déterminée par leur position relative à un instant donné, et ce quelle que soit la distance les séparant. Ce caractère instantané est incompatible avec l'idée de la relativité restreinte proposée par Einstein en 1905. En effet, selon cette dernière, aucune information ne peut se propager plus vite que la vitesse de la lumière dans le vide. Par ailleurs, le principe de l'action à distance repose sur celui de la simultanéité de deux événements : la force que le Soleil exerce sur la Terre à un instant donné est déterminée par leurs propriétés « à cet instant ». La relativité restreinte stipule que le concept de simultanéité de deux événements n'est pas défini, la perception de la simultanéité étant différente d'un observateur à un autre pour peu que ceux-ci soient animés d'une vitesse relative non nulle. Ces contradictions amènent Einstein dès 1907 à réfléchir à une théorie de la gravitation qui soit compatible avec la relativité restreinte. Le résultat de sa quête est la théorie de la relativité générale.

De la relativité de Galilée à la relativité restreinte

Au XVI^e siècle, Galilée affirme et explique que les lois de la physique sont les mêmes dans des référentiels en translation rectiligne et uniforme les uns par rapport aux autres. C'est le principe de relativité (de Galilée).

Il utilisera aussi l'additivité des vitesses, selon laquelle n'importe quelle vitesse peut être atteinte, le tout n'étant qu'une question de moyens. Si une balle roule à 10 km/h dans un train (et dans le sens de la marche) qui va lui-même à 100 km/h par rapport au sol, alors la balle va à 110 km/h par rapport au sol.

Dans sa Mécanique, Isaac Newton présupposait que les corps étaient dotés d’une vitesse absolue, autrement dit qu’ils étaient soit « réellement » au repos, soit « réellement » en mouvement. Il remarqua aussi que ces vitesses absolues étaient non mesurables autrement que relativement aux vitesses des autres corps (de la même manière, la position d’un corps n’était mesurable que relativement à celle d’un autre corps, etc.). En conséquence, toutes les lois de la mécanique newtonienne devaient opérer à l’identique quel que soit le corps considéré et quel que soit son mouvement.

Cependant, Newton pensait que sa théorie ne pouvait avoir de sens sans l’existence d’un référentiel fixe absolu dans lequel la vitesse de tout corps pourrait être mesurée, même si celui-ci ne pouvait être détecté.

En fait, il est possible en pratique de bâtir une mécanique newtonienne sans cette hypothèse : la théorie résultante (nommée d’ailleurs relativité galiléenne) n’a d’ailleurs pas d’intérêt opérationnel particulier et ne doit pas être confondue avec la relativité d'Einstein qui implique en plus la constance de la vitesse de la lumière dans tous les référentiels et en moins l’hypothèse galiléenne que les vitesses relatives s’additionnent (ces deux postulats sont en effet mutuellement incompatibles).

Au XIX^e siècle, le physicien écossais James Clerk Maxwell formula un ensemble d’équations, les équations du champ électromagnétique, qui conduisait à prédire la propagation d'ondes électromagnétiques de vitesse dans un milieu électrostatique de constante ε₀ et magnétostatique de constante μ₀. Cette vitesse phénoménalement élevée, même dans un milieu raréfié comme l'air, avait la même valeur que la vitesse de propagation de la lumière. Il proposa que la lumière ne soit rien d'autre qu'une onde électromagnétique.

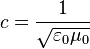
Les théories corpusculaires de la lumière semblaient compatibles avec le principe de relativité de Galilée ainsi que la théorie de Maxwell qui penchait en faveur de l'existence d'un éther luminifère envisagé par Huygens. Mesurer la vitesse du système solaire par rapport à ce milieu élastique fut l'objet des expériences d’interférométrie menées par Michelson et Morley. Leurs expériences ont démontré que le vent apparent d'éther était nul, quelle que soit la période de l'année. Supposer que l'éther était constamment accroché à la Terre aurait été une remise en cause trop grave du principe de relativité de Galilée. D'autre part, l'éther présentait l'inconvénient d'être à la fois impalpable et très rigide puisque capable de propager les ondes à une vitesse phénoménale.

Il fallut attendre Albert Einstein en 1905 pour remettre en cause radicalement la notion d'éther, porter au plus haut le principe de relativité de Galilée en postulant que les équations de Maxwell obéissent elles-mêmes à ce principe, et en tirer les conséquences révolutionnaires dans un article resté célèbre : De l’électrodynamique des corps en mouvement.

C'est la naissance de la relativité restreinte :

• le principe de relativité de Galilée est conservé ;
• l'invariance des équations de Maxwell entraîne immédiatement la constance de la vitesse de la lumière c dans tous les référentiels galiléens : l'additivité des vitesses n'est plus vraie et la vitesse de la lumière est inatteignable (sauf pour la lumière, qu'elle soit considérée comme une onde ou comme constituée de photons, particules de masse nulle) ;
• les mesures de longueur, d'intervalle de temps, (et de vitesse) ne sont pas les mêmes suivant le référentiel de l'observateur : mesurer la longueur du wagon donne des résultats différents suivant que l'on est dedans ou que l'on est immobile au sol (mais ce n'est pas le cas pour la largeur du wagon, longueur perpendiculaire à la vitesse) ; de même pour l'écoulement du temps ; le champ électrique devient magnétique et réciproquement. Toutes ces transformations des systèmes de coordonnées du continuum espace-temps et du champ électromagnétique sont formalisées par les transformations de Lorentz (paradoxalement mises au point par Lorentz et Henri Poincaré pour défendre l'existence de l'éther) ;
• la notion de temps absolu disparaît : deux horloges identiques situées dans deux référentiels galiléens différents ne battent pas au même rythme.

En écrivant l'expression de l'énergie cinétique d'un corps de masse m de la manière la plus simple respectant le principe de relativité, Einstein a fait apparaître une énergie au repos E=mc² qui se manifestera par la suite dans les phénomènes de fusion et de fission nucléaires.

De la relativité restreinte à la relativité générale

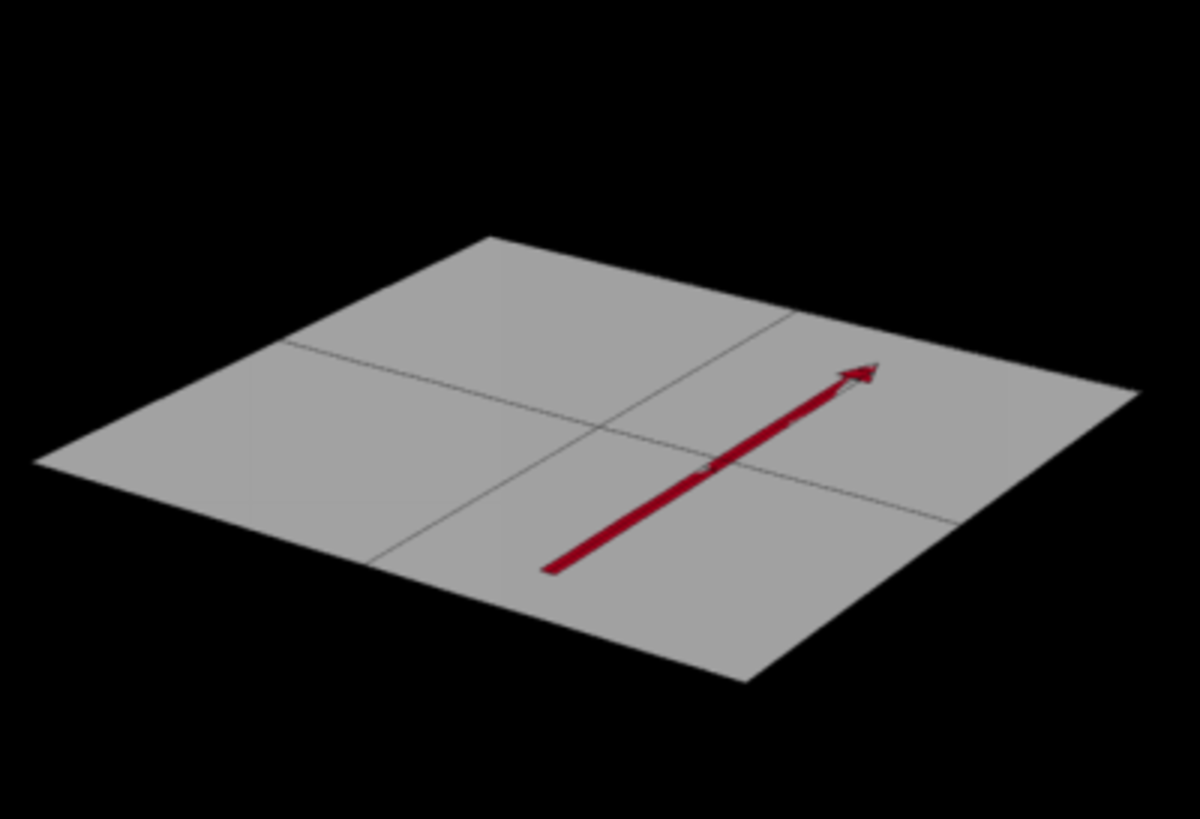
La théorie de la relativité restreinte (1905) modifiait les équations utilisées pour comparer les mesures de longueur et de durée faites dans différents référentiels en mouvement les uns par rapport aux autres. Cela eut pour conséquence que la physique ne pouvait plus traiter le temps et l’espace séparément, mais seulement comme un espace à quatre dimensions, appelé l'espace-temps de Minkowski.

En effet, lors de mouvements à des vitesses non négligeables devant c (vitesse de la lumière dans le vide), temps et espace s'altèrent de façon liée, un peu comme deux coordonnées d'un point en géométrie analytique s'altèrent de façon liée lorsqu’on pivote les axes du repère.

Espace plat

Par exemple, en géométrie euclidienne habituelle la distance entre deux points de coordonnées et vérifie (avec , etc.), mais dans l'espace de Minkowski deux points sont repérés par les coordonnées et , où et sont les coordonnées de temps, et la « distance » entre ces points vérifie . Ce calcul donne une « distance » nulle entre deux points du parcours d'un rayon lumineux. Il donne aussi toutes les mesures de longueurs matérielles, des intervalles de temps, des vitesses en relativité restreinte, qui suscitent toujours l'étonnement.

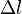
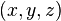
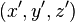
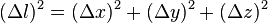
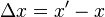
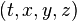
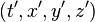
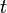
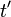
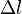
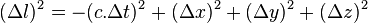
L'espace-temps de Minkowski étant néanmoins de courbure nulle (c'est-à-dire plat) on le qualifie d'espace pseudo euclidien.

Tel devait être, pour Einstein, l'espace sans gravitation (et sans accélération pour l'observateur). La gravitation newtonienne, se propageant instantanément, n'est pas compatible : Einstein se mit donc en quête d'une nouvelle théorie de la gravitation.

Il admit l'égalité entre la masse gravitationnelle et la masse inertielle comme hypothèse, la fameuse formule E = mc² autorisant alors à utiliser l'énergie totale d'un corps en lieu et place de sa masse. Ce sera fait grâce à l'outil mathématique nommé tenseur énergie.

Expert en expériences par la pensée, il imagina un disque en rotation regardé par un expérimentateur placé en son centre et tournant avec : comme pour Huygens, il y a une force centrifuge au niveau du périmètre qui est perçue comme une force gravitationnelle (car la masse gravifique et la masse inerte sont égales par hypothèse). De plus, en voulant rester dans le cadre de la relativité restreinte, il conclut que l'observateur doit constater la réduction du périmètre mais pas du rayon : ce n'est pas possible dans un espace plat. Conclusion : la gravitation oblige à utiliser une géométrie non-euclidienne.

Einstein imagina un expérimentateur enfermé dans un ascenseur aux parois opaques, subissant une montée à accélération constante : l'ascenseur d'Einstein dans lequel il est impossible pour une personne de savoir s'il y a accélération constante ou bien attraction gravitationnelle constante (car la masse gravifique et la masse inerte sont égales par hypothèse). Conclusion : équivalence locale entre mouvement accéléré et gravitation, ce qui devait se retrouver dans les équations différentielles de la nouvelle théorie. C'est son principe d'équivalence.

Enfin, Einstein voulait trouver une expression des lois de la nature (à l'époque : dynamique, gravitation et électromagnétisme) qui soit inchangée quel que soit le référentiel (accéléré ou galiléen, etc.) : c'est la relativité galiléenne généralisée à tous les repères (on nomme cela la covariance).

La grande difficulté étant de mettre ces principes sous forme mathématique, il en discuta avec David Hilbert qui, d'abord dubitatif, faillit lui ravir la vedette en trouvant la théorie en même temps que lui (voir : Controverse sur la paternité de la relativité).

Géodésiques

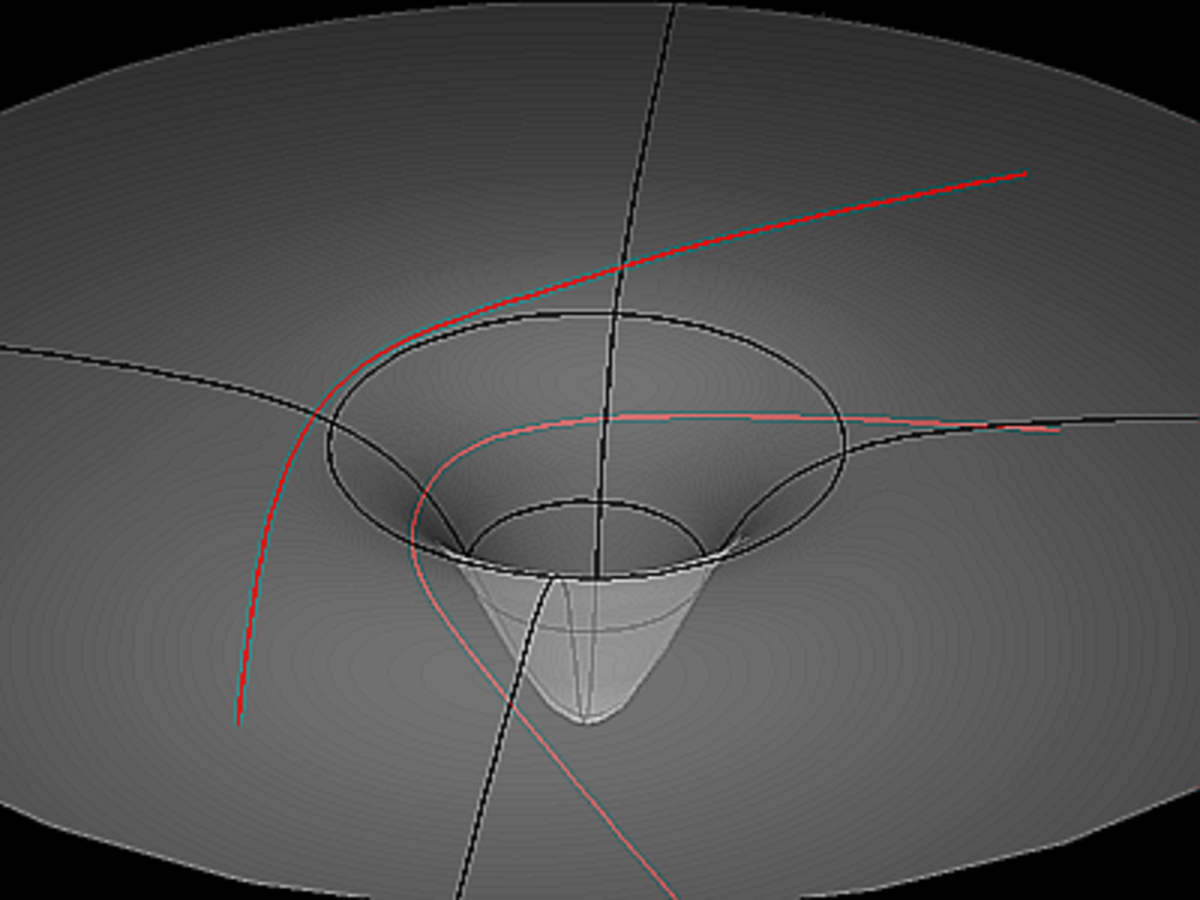
La relativité générale ajouta à la relativité restreinte que la présence de matière pouvait déformer localement l’espace-temps lui-même (et non pas juste les trajectoires), de telle manière que des trajectoires dites géodésiques — c'est-à-dire intuitivement de longueur minimale — à travers l’espace-temps ont des propriétés de courbure dans l’espace et le temps. Le calcul de la « distance » dans cet espace-temps courbé est plus compliqué qu'en relativité restreinte, en fait la formule de la « distance » est créée par la formule de la courbure, et vice-versa.

Les géodésiques sont les trajectoires vérifiant le principe de moindre action, suivies par les particules test (c'est-à-dire dont l'influence sur le champ de gravitation dans lequel elles se déplacent est négligeable, ce qui est le cas par exemple d'un satellite artificiel autour de la Terre ou bien d'un photon passant à côté du Soleil mais pas d'une étoile orbitant autour d'une autre dans un système binaire oscillant rapidement), elles ont donc une importance pratique très importante pour la compréhension intuitive d'un espace courbe.

Conséquences théoriques et observations

• Einstein calcula immédiatement (1915) la déviation des positions apparentes des étoiles par le Soleil : le 29 mai 1919, les mesures furent faites par Sir Arthur Eddington lors d’une éclipse solaire, et malgré quelques imprécisions de mesure, cela constitua une première confirmation de la théorie.
• Cette théorie prévoit une rotation lente de l'ellipse de révolution de Mercure qui concorde parfaitement avec les observations.
• La gravitation (forte) d'une planète doit y contracter les longueurs observées depuis une position lointaine. Cela n'a pu être observé directement à ce jour.
• La gravitation doit ralentir le temps, donc modifier les fréquences et les longueurs d'onde des rayonnements émis : on peut citer par exemple une expérience menée par Pound et Rebka à l'université Harvard (1959), qui a permis de détecter un changement de la longueur d'onde d’une source monochromatique de Cobalt provoqué par le champ gravitationnel terrestre sur une altitude de 22,5 mètres .
• Schwarzschild, en trouvant en 1916 une solution exacte des équations de la gravitation, a montré qu'il pouvait exister des conditions où un phénomène de trou noir apparaissait. L'astronomie observe des phénomènes similaires.
• Dans certaines conditions, des ondes gravitationnelles, discrètes, doivent se propager dans l'espace. L'expérience franco-italienne Virgo cherche à en détecter.
• Autre conséquence pratique de la relativité générale : les horloges atomiques en orbite autour de la Terre du système de positionnement GPS (Global Positioning System) nécessitent une correction pour le ralentissement dû à la gravité terrestre.

Pour résumer cette théorie, Einstein amusa un public de journalistes : « Imaginez que vous regardez loin, très loin devant vous et que vous avez une très bonne vue, une très très bonne vue, alors vous arriverez à voir… votre dos ».